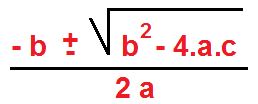Ya todos conocemos la ecuación general de la recta. y = ax + b, donde la a es la pendiente y b es la ordenada al orígen. Sin embargo algunas veces nos piden la ecuación segmentaria de (más…)
Funciones
Función cuadrática
Logaritmos. Propiedades y Ejercicios
El Logaritmo es una función similar a la potenciación. El logaritmo de un número en cierta base, da como resultado otro número tal que la base elevada a este resultado es igual al primer número.
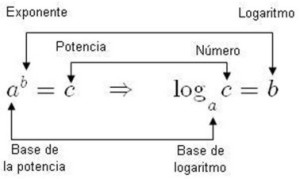
Al valor que se le calcula el logaritmo se le llama argumento. Estas son las partes de un logaritmo para entender mejor la definición.
Al valor ¨C¨se lo llama argumento, «a», representa la base y «b» es el resultado del logaritmo. Como vemos a la izquierda, al elevar al «a» a la «b» nos da de nuevo el valor C, o sea, el argumento. Por esto decimos que la función logaritmo es (más…)