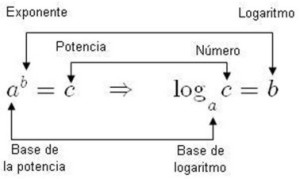
El Logaritmo es una función similar a la potenciación. El logaritmo de un número en cierta base, da como resultado otro número tal que la base elevada a este resultado es igual al primer número.
Al valor que se le calcula el logaritmo se le llama argumento. Estas son las partes de un logaritmo para entender mejor la definición.
Al valor ¨C¨se lo llama argumento, «a», representa la base y «b» es el resultado del logaritmo. Como vemos a la izquierda, al elevar al «a» a la «b» nos da de nuevo el valor C, o sea, el argumento. Por esto decimos que la función logaritmo essimilar a la potenciación.
Ejemplos:
Como vemos en los 3 casos, a la derecha vemos la confirmación del porque los resultados son los que se dan. Cuando calculamos un logaritmo, lo corroboramos elevando la base al resultado para que nos de el argumento. No siempre es necesario poner la confirmación de nuestros resultados, pero para los fines de explicación sirve. A esto le llamamos calcular logaritmos por definición.
No siempre se puede calcular logaritmos. Hay restricciones que se deben conocer.
No existen los logaritmos de números negativos. O sea, nunca el argumento debe ser menor que cero. Ya que no existe ningún número tal que la base elevada a ese número nos de un valor negativo. La base por otra parte debe ser mayor a cero y diferente a uno.
Los logaritmos están sujetos a 4 propiedades fundamentales que el alumno debe conocer.
El logaritmo de un producto es igual a la suma de los logaritmos o viceversa. Siempre y cuando tengan la misma base. Es decir, si a y b tuvieran bases distintas, no se aplica ni esta propiedad ni las tres restantes que se ven en el gráfico. Para aplicar las cuatro propiedades de logaritmos los argumentos deben tener la misma base.
En el segundo caso vemos que el logaritmo de un cociente e sigual a la resta de los logaritmos.
El logaritmo de un número (a) elevado a un exponente (b) es igual al exponente (b) multiplicado por el logaritmo de (a).
El logaritmo de una raíz de (a) es igual al logaritmo del radicando (a) dividido por el índice (b).
Otra cuestión importante que el alumno debe saber es que las propiedades de los logaritmos las podemos usar para ambos sentidos, o sea que por ejemplo, si tenemos una suma de logaritmos, la podemos pasar a un producto o al revés, de un producto podemos expresar la suma. Esto dependerá de que nos pidan en los ejercicios.
En los logaritmos en los que no veamos la base, significa que se trata de la base 10. Es como en las raíces cuadradas, no vemos que el índice sea 2 pero sabemos que es 2. Otro caso especial son los logaritmos llamados naturales. En esos casos, la base es el número e que es un número irracional muy conocido en matemática. Tiene un valor aproximado de 2,718….
Veremos un ejemplo de como se puede resolver un ejercicio de logaritmos.
En este ejercicio vemos que en primer lugar tenemos un cociente, entonces aplicamos la propiedad del cociente quedando una resta. A su vez, tenemos dos productos uno en cada termino de la resta. Lo transformamos en sumas. Luego sacamos los paréntesis y se cambian los signos del término derecho del segundo paso. Por último en el tercer paso, seguimos aplicando algunas propiedades. El exponente 4 pasa multiplicando, el índice 3 del radical queda dividiendo y el exponente 40 pasa multiplicando. El alumno puede terminar el ejercicio. Rta: -27.775
A continuación veremos un par de ejemplos de como se resuelven las ecuaciones logarítmicas. Ecuaciones logarítmicas son aquellas en las que la incógnita «x» está afectada dentro de un logaritmo o están bajo la influencia de este.
Aquí tenemos un logaritmo natural. La base «e» por definición de logaritmo, la elevamos al resultado (2) dando el argumento (7x – 1). De esta manera eliminamos el logaritmo y nos queda una ecuación muy sencilla de resolver a partir del tercer paso como se muestra. Solo despejamos la x y listo.
Aquí vemos una situación diferente ya que no tenemos un logaritmo sino tres. En dos figuran la x en el otro no.
El número 2 que multiplica al primer log del segundo término lo elevamos como exponente de (x+3) por propiedad. En el tercer paso aplicamos la propiedad de la resta en el segundo término para pasarlo a un cociente. Ahora tenemos un log de cada lado o miembro. Cuando tenemos una igualdad y un log de cada miembro lo eliminamos directamente ya que se trata de una igualdad y son log de la misma base. A partir del cuarto paso, tenemos una ecuación común que deriva en una de segundo grado al ordenar los términos. Aplicamos baskara para hallar los valores de «x» y ya esta.
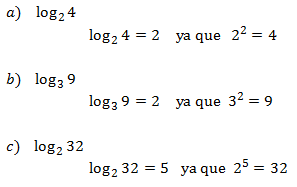


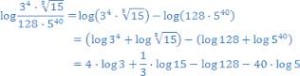
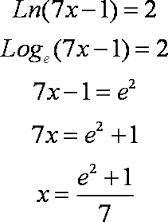
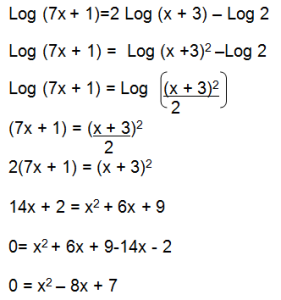

Hola, me parece bien tu explicación, solo que no me queda claro que en si el logaritmo, se en que se usa pero no que es :/
Es una función similar a la potencia
Hola
Esta muy linda tu pagina.
Te comento que lo que he publicado en mi sitio web es libre y se puede usar. Me hubiera parecido mas honesto de tu parte si cuando utilizas mis materiales, por lo menos citas las fuentes.
Saludos
Hola, decime puntualmente que material.
Hola, tengo una inquietud en el último ejercicio en el que se aplica baskara. Si me podrían explicar el sexto paso del segundo término y de donde sale el 6X. Muchas gracias.
Es porque tenes que resolver un cuadrado de binomio. Al quedarte (x+3) al cuadrado haces cuadrado de binomio
exijo que expliquen las formulas de el logaritmo, pero con letras
Primero se dice hola. Y segundo no sos o eres quien para exigir. Las cosas se piden con humildad. Siempre acepto las críticas constructivas y hasta alguna corrección. Pero ante todo el respeto y la humildad para pedir cosas. Por otro lado el artículo se entiende perfectamente.
buenas noches me agrada su pagina escribo desde VENEZUELA
Hola Donny. Sos muy amable.
hola esta muy bien su explicación,
en mi caso me cuesta particularmente mucho razonar los problemas y me pierdo (repito por mi no porque no este claro) y no se si seria posible, por favor, explicar algún problema de pH en los que intervengan logaritmos.
Hola Vero. Si buscas en este blog en la parte de química verás ejercicios de pH.
Hola, me podría ayudar, es que tengo que realizar una exposición sobre las aplicaciones de logaritmo. Me puede dar un resumen con ejemplos por favor.
Eso es un trabajo que demanda tiempo Marcelo. Pero sacalo directamente de mi post que leíste ahí esta todo.
Hola buenas tardes, me llamo max tengo 15 años quisiera que me ayude con este problema no lo entendí muy bien, su articulo me ayudo pero aun no comprendo el tema seria muy amable de explicármelo MUCHAS GRACIAS
EL Co-60 actualmente es empleado en tratamientos oncológicos : su tiempo de vida media es de 5,27 años
después de 26.35años permanecen 11g de Co-60 ¿Cuántos miligramos de la muestra de Co-60 se tenía
inicialmente?
Hola Max. Esto no es fácil explicarlo acá. Responde a un modelo de ecuaciones exponenciales. Hay que ver si vos tenes que armar la ecuación, que es lo más probable, o te la dieron para que despejes C inicial.