El teorema de Pitágoras fue descubierto por el matemático griego que lleva su mismo nombre allá por el siglo VI antes de Cristo. Pitágoras quizá sea el matemático más reconocido y antiguo en el mundo de las matemáticas.
Es sencillo y a su vez de una enorme aplicación hasta hoy en la actualidad y se seguirá usando. Este teorema se aplica a los triángulos rectángulos, no a cualquier triangulo, debemos aclarar. Los triángulos rectángulos son aquellos que tienen un angulo de 90°.
Antes de entrar al teorema veremos a continuación en la figura los 3 lados de un triángulo rectángulo. El lado más largo se llama hipotenusa y los otros dos Sigue leyendo Teorema de Pitágoras. Ejercicios resueltos.
Categoría: Matemática
Como calcular el dominio e imágen de las funciones.
Cuando nos piden calcular el dominio de una función, lo que nos están pidiendo es calcular el campo de existencia de esta a lo largo del eje x. Es decir, si para un elemento de x existe su correspondiente en “Y”, dicho elemento de X es parte del dominio. Para aclarar este concepto veremos algunos ejemplos. También veremos el concepto de imagen o codominio que es la existencia de la función a lo largo del eje «Y».
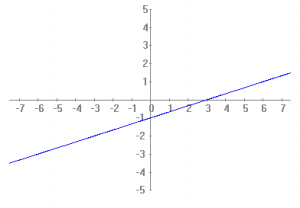
Función lineal:
Aquí observamos que para todo elemento de «X» habrá otro correspondiente en «Y». Más allá de que nos de la impresión de que en el gráfico la recta solo existe en una parte. En realidad el dominio se extiende desde Sigue leyendo Como calcular el dominio e imágen de las funciones.
Función Cuadrática
La función cuadrática es un tema muy común en matemática. Se la puede expresar en 3 formas distintas.
Forma polinómica: a X2 + b X + C
Forma canónica: a (X – Xv )2 + Yv
Forma factorizada: a (X – X1) . (X – X2)
Vamos a analizar primero la forma polinómica.
Al estudiar las funciones cuadráticas debemos saber cómo graficarlas y como analizarlas.
Para graficarlas solo basta con conocer los llamados puntos característicos. Estos son las raíces que están Sigue leyendo Función Cuadrática
Números Complejos
Operaciones con números complejos
Los números complejos constituyen el campo más grande de los números ya que contienen a todos los reales y a los imaginarios.
Los números imaginarios surgen de la imposibilidad de calcular las raíces pares de los números negativos. Como por ejemplo la raíz cuadrada de -9 no tiene solución ya que ni el +3 al cuadrado ni el -3 al cuadrado daría -9. La unidad imagnaria es «i» y es igual a la raíz cuadrada de -1.
El conjunto de los números complejos se designa generalmente con la letra C. pero en los ejercicios de matemática, a cada uno los vemos simbólicamente con la letra Z. Por ejemplo:
Z1 = 2 + 3i Z2 = -4 + 5i
Vemos que cada uno tiene una parte real y una imaginaria.
Los números complejos están sujetos a las mismas operaciones que practicamos con los números enteros. Suma (adición), Resta (sustracción), Producto (multiplicación) y Cociente (división). A continuación mostraremos ejemplos de Sigue leyendo Números Complejos
Ecuaciones de primer grado
El término ecuación significa despejar o hallar el valor desconocido en una expresión matemática. Dicho valor desconocido esta simbolizado con una letra X aunque a veces puede estar representado por otras como a, b, c, etc. De todas maneras el concepto es el mismo. Las expresiones constan de dos miembros, derecho e izquierdo, separados por un igual. En uno de esos miembros o en ambos pueden figurar las incógnitas. En este post explicaremos las ecuaciones de primer grado, es decir, la X esta elevada a la uno. Daremos a continuación los principales ejemplos con los que nos podemos encontrar.
Por ejemplo:
X + 3 = 9
Este caso es muy sencillo. Solo debemos despejar a la X, es decir, quitar lo que esta del mismo lado de la igualdad que afecta a la X y pasarlo al otro lado para que la X quede sola. Cada término que movemos lo pasamos al otro lado de la igualdad con la operación contraria. En este caso, el 3 estaba sumando, entonces lo pasamos a la derecha restando. En el caso que multiplicaría se lo pasaría dividiendo.
X = 9 – 3
X = 6
Otro ejemplo es cuando la X esta con un número adelante. Esto significa que la multiplica. También indica cantidad de X.
2 X + 3 = 15
Primero pasamos el 3 restando y luego el 2 que multiplica pasa dividiendo a la derecha.
2 X = 15 – 3
2 X = 12
X = 12 / 2
X = 6
A veces podemos tener las X a ambos lados de los miembros. Ejemplo:
6 X – 5 = 2 X + 3
Lo que debemos hacer primero es agrupar las X a la izquierda y los términos independientes, o sea, los números solos, a la derecha. También se pueden agrupar de forma inversa, es decir, las X a la derecha y los términos independientes a la izquierda. Observemos los cambios de signo que afectan a los términos que se mueven. El 2 X pasa a ser negativo y el – 5 pasa a ser positivo.
6 X – 2 X = 3 + 5
4 X = 8
X = 8 / 4
X = 2
No te pierdas este tutorial para entender mejor a las ecuaciones.