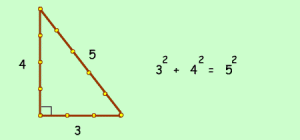El teorema de Pitágoras fue descubierto por el matemático griego que lleva su mismo nombre allá por el siglo VI antes de Cristo. Pitágoras quizá sea el matemático más reconocido y antiguo en el mundo de las matemáticas.
Es sencillo y a su vez de una enorme aplicación hasta hoy en la actualidad y se seguirá usando. Este teorema se aplica a los triángulos rectángulos, no a cualquier triangulo, debemos aclarar. Los triángulos rectángulos son aquellos que tienen un angulo de 90°.
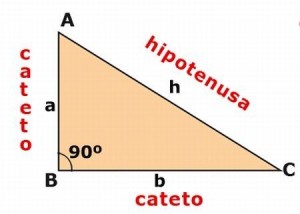
Antes de entrar al teorema veremos a continuación en la figura los 3 lados de un triángulo rectángulo. El lado más largo se llama hipotenusa y los otros dos son los catetos.
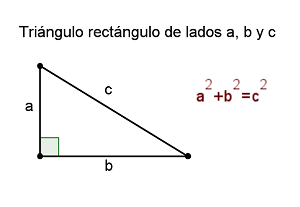
El Teorema de Pitágoras establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Veremos con un ejemplo:
Mediante un calculo sencillo podemos verificar esta igualdad. Ahora vamos a suponer que nos hubieran dado el valor de la hipotenusa, o sea, el 5. Si la hipotenusa hubiera sido una incógnita hubiera sido fácil hallarla mediante una sencilla ecuación:
X² = 3² + 4²
X = √ (3² + 4²)
X = √ (25)
X = 5
También las incógnitas podrían haber sido los catetos y se hubiera procedido de una manera similar.
La aplicación más importante y común en la que se utiliza el teorema de Pitágoras es con un instrumento llamado teodolito. Este se encarga de medir distancias largas y no tan largas de una manera practica evitando hacerlas directamente con un instrumento de cinta lo cual no sería nada practico y llevaría mucho tiempo y mucho error. El teodolito es un instrumento óptico que mide ángulos y por calculo se determina la distancia a cierto punto o la altura.
No te pierdas el siguiente vídeo para que no te queden más dudas. Verás como se calculan la hipotenusa y los catetos.
Ejercicios para realizar:
Calcula la hipotenusa en un triángulo que tiene catetos a = 5 cm y b = 8 cm. Rta: 9.43 cm
Calcula el cateto a si el cateto b = 9 cm y la hipotenusa es de 12 cm Rta: 7.94 cm
Calcula el cateto b si el cateto a es de 4 cm y la hipotenusa es de 14 cm Rta: 13.42 cm
Tema Relacionado:
Calculo de Seno, Coseno y Tangente en Triángulos Rectángulos.