En análisis de funciones el concepto de conjunto de positividad y negatividad es muy pedido y aquí explicaremos que significa y como determinarlo.

Lo primero que debemos determinar son las raíces, que para recordar, son aquellos valores en donde la función toca o atraviesa al eje x. La mejor manera de explicar esto es con ejemplos que a continuación mostraremos.

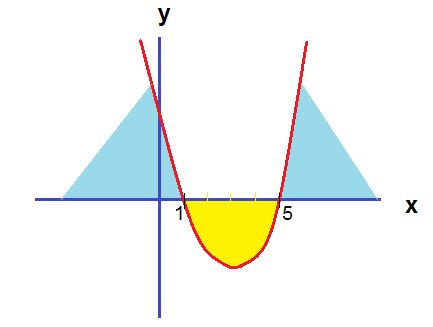
Aquí tenemos una función cuadrática representada por una parábola descripta por la línea roja. Las raíces son los puntos 1 y 5 sobres el eje X. Todo conjunto de Positividad y Negatividad se lee sobre el eje X. El de Positividad se encuentra representado por los valores de X para los que la función se halla por encima del eje X. En este caso lo representamos de color celeste. Mientras que la parte coloreada de amarillo representa al Conjunto de negatividad ya que entre las raíces x=1 y X=5 la función pasa por debajo del eje X. Cuando debemos escribir a dichos conjuntos lo debemos hacer de la siguiente manera.

C+ = (-∞ , 1) U ( 5 , +∞)

Se lee: Conjunto de Positividad es de menos infinito hasta 1 unión de 5 a más infinito. Es decir, son dos tramos separados por el conjunto de negatividad. Como no es un intervalo continuado ponemos la palabra unión.

C- : (1 , 5)

Se lee: Conjunto de Negatividad es de 1 a 5.

A continuación veremos el siguiente ejemplo:

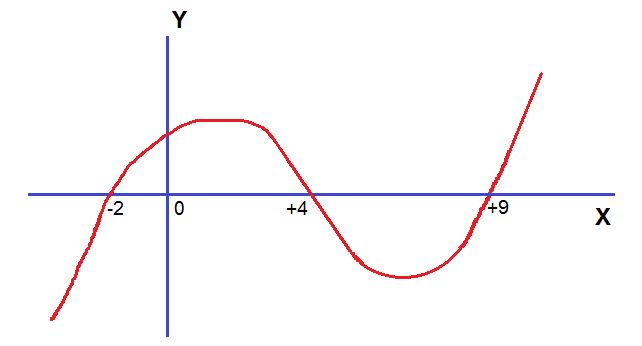
En este caso no es necesario colorear nada, aunque es algo más complejo que el caso anterior, pero nada difícil. Observemos que entre -2 y +4 de X la función se encuentra por ensima del eje X. Lo mismo sucede desde el +9 hacia la derecha. Entre el menos infinito y -2 y entre +4 y +9 la función está por debajo del eje X. Ahora solo queda expresarlo.

C+ : (-2 , +4) U (+9 , +∞)

C- : (-∞ , -2) U ( +4 , +9)

Espero que este artículo te haya servido. Deja tus comentarios y puedes suscribirte al boletín para recibir nuestros últimos artículos. Éxitos.

Profesor: Patricio Arroyo.