Las ecuaciones logarítmicas son aquellas en las que la incógnita esta afectada dentro de un logaritmo. Por lo tanto, para resolverlas debemos manejar bien el concepto y las propiedades de los logaritmos. A continuación veremos algunos ejemplos para que esto quede bien claro.

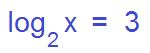
Aquí vemos que la incógnita (x) es el argumento del logaritmo. Al haber un solo logaritmo, directamente aplicamos el concepto de logaritmo para poder despejar nuestra incógnita. . La base elevada al resultado es igual al argumento. La base en este caso es 2 y el resultado es el 3. Por lo tanto 2 elevado a la 3 es igual a X.

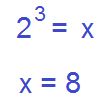
En otros casos algo más complejos tenemos más de un logaritmo como en el siguiente caso.

Observamos que se trata de una suma de logaritmos de la misma base (2). Cuando tenemos este caso aplicamos la propiedad de la suma. La suma de logaritmos de la misma base es igual al logaritmo en la misma base del producto de los argumentos. En este ejemplo queda de la siguiente manera.

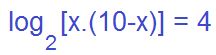
Ahora tenemos la ventaja de tener un solo logaritmo y no dos logaritmos como antes. Para esto se aplica la propiedad. Aplicamos la definición que dice que la base elevada al resultado da el argumento.

A continuación resolvemos la expresión hasta que obtenemos una ecuación de segundo grado. 2 a la cuarta es 16 y a la derecha aplicamos la propiedad distributiva. Reordenamos e igualamos 0. Por último resolvemos la ecuación cuadrática con baskara quedando los resultados que ven a continuación.

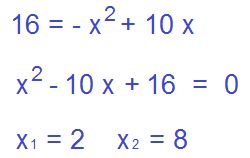
Otro ejemplo. Ecuación logarítmica con resta de logaritmos.

En casos así aplicamos la propiedad de la resta. La resta de dos logaritmos de igual base es igual al logaritmo del producto de sus argumentos en la misma base.

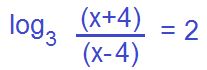
Ahora aplicamos la definición de logaritmo.

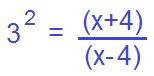
Ya nos liberamos del logaritmo. Solo resolvemos esta sencilla ecuación. 3 al cuadrado es 9. El denominador lo pasamos a la izquierda multiplicando y despejamos x.

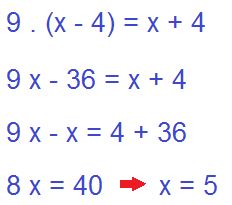
Hay mas variabilidad de ejercicios, pero estos casos son los más frecuentes. Es importante que sepas las propiedades del los logaritmos para poder resolver las ecuaciones logarítmicas como lo habíamos mencionado. Espero que te haya resultado útil este artículo. Deja tus dudas y comentarios. Éxitos.