Las ecuaciones exponenciales son aquellas en las que la incógnita esta como exponente, de ahí el nombre de exponenciales.
Las hay de menor y de mayor complejidad. A continuación explicaremos algunos ejemplos.
Aquí observamos que podemos expresar al 16 como potencia del 2. Entonces quedan las mismas bases a ambos lados de la igualdad. Como se trata de una igualdad, los exponentes también deben ser iguales. De esta forma deducimos fácilmente que X = 4.
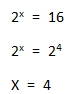
En este otro caso, procedemos de manera similar. Sabemos que el 27 es potencia del 3, entonces transformaremos a esta fracción para que coincidan las bases y por consiguiente hallemos de inmediato al valor de la x.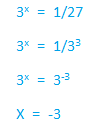
Recordemos que si tenemos un exponente negativo en el denominador como en este caso, podemos colocarlo en el numerador para que quede positivo.
Hay otras ecuaciones exponenciales que merecen un mayor desarrollo.
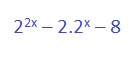
Podemos ver que los exponentes no son iguales ya que uno es 2.x y el otro es 2 a la x. No lo podemos juntar, sin embargo, el primero lo podemos expresar de otra forma.
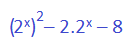
El 2 por afuera y la x por dentro en el primer término. Como se puede observar, esta ecuación tiene ahora la forma de una ecuación cuadrática de fácil resolución. Ya que la base es 2 a la x, una esta al cuadrado y la otra no. Tenemos el término cuadrático y el lineal.
Generalmente lo que se hace es una sustitución con otra letra para reemplazar al término exponencial.
Por ejemplo la T:
![]()
![]()
La resolución de esta ecuación de baskara arroja dos resultados:
T = – 2
T = + 4
Entonces volvemos a reemplazar para igualar con 2 a la x, ya que a nosotros nos importa el valor de x y no el valor de T. La T solo fue algo intermediario.
2x = -2
2x = +4
La primera no tiene solución, ya que ningún exponente de base positiva nos dará como resultado un valor negativo. En la segunda vemos que la respuesta es 2, ya que el 4 se expresa como 2².