Los triángulos oblicuángulos son aquellos que no tienen ningún ángulo interior de 90° a diferencia de los triángulos rectángulos.
Resolver un triángulo oblicuángulo implica hallar a todos los lados y ángulos interiores que nos pidan. Las fórmulas que se usan para esto difieren de las usadas para resolver a los triángulos rectángulos, como lo hemos visto en otro artículo.
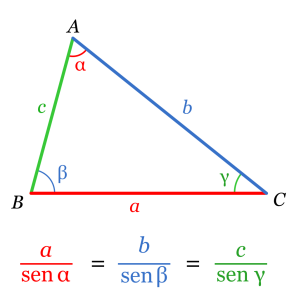
Teorema del Seno:
Establece la relación que hay entre cada lado y el seno del ángulo opuesto a dicho lado, y estas tres relaciones, a su vez, son iguales entre si. En el siguiente gráfico lo vemos bien.
Con estas relaciones podemos calcular lados o ángulos que falten. De estos tres miembros obviamente usaremos solo a dos, dependiendo de cuales sean los datos de los que disponemos.
A veces no nos alcanza con el Teorema del Seno para resolver problemas, por no adecuarse al problema que tenemos y debemos usar el Teorema del Coseno. Las fórmulas figuran a continuación.
Como vemos son muy parecidas, solo que cambian el orden de los lados y el ángulo que se forma con esos lados. Por ejemplo en la primera, empieza con el lado a, entonces el ángulo que figura al final es el opuesto, el A. Los otros dos lados a su vez, son los que forman el ángulo A. De la misma manera usamos el razonamiento para las otras dos fórmulas.
Veamos algunos ejemplos.
1) Calcula los lados y el ángulo que falta en el siguiente triángulo oblicuángulo.
Como vemos, podemos empezar calculando el lado b o el c, utilizando el teorema del seno. Para el lado b tenemos:
b/sen75° = a/sen40°
b = (a/sen40°) x sen 75°
b = (12/sen40°) x sen 75°
b = 12/0.643 x 0.966
b = 18
Para calcular el lado c hacemos:
c / sen C = 12 / sen 40°
El ángulo C es fácil de calcular ya que tenemos a los otros dos. Sabiendo que la suma de los tres nos da 180°:
C = 180° – 40° – 75°
C = 65°
c = (12 / sen 40°) x sen 65°
c = (12/0,643) x 0,906
c = 16.91
2) Calcula el lado y los ángulos que faltan del siguiente triángulo oblicuángulo.
Como vemos aquí, no se puede utilizar el teorema del seno ya que siempre nos faltara un dato. Tendremos una ecuación con dos incógnitas y eso no lo podremos resolver. Por ejemplo, tenemos el lado c pero no su ángulo opuesto (C) o tenemos el ángulo (B) pero no su lado b. Lo mismo pasa con la relación (A) y a, falta el ángulo. Entonces en este caso, el teorema del coseno es el indicado ya que lo puede resolver.
Para hallar el lado b procedemos así:
b² = a² + c² – 2.a.c.cosB
b² = 1200² + 700² – 2.1200.700. cos 108°
b² = 1440000 + 490000 – 1680000.-0.309
b² = 1930000 + 519120
b² = 2449120
b = 1565 metros
Ahora podemos sacar el ángulo A o el C. Para el ángulo A hacemos:
a² = b² + c² – 2.b.c. cosA
1200² = 1565² + 700² – 2.700.1565.cosA
1440000 = 2449225 + 490000 – 2191000 cosA
-1499225 = – 2191000 cosA
cosA = -1499225/-2191000
cosA = 0.684
Ahora usamos la función inversa para obtener el ángulo deseado.
A = arc cos 0.684
A = 46° 49´19″
Para calcular el ángulo C solo le restamos a 180° el valor de los otros dos. Recordemos que la suma de los tres ángulos interiores de todo triángulo da 180°
C = 180° – 108° – 46° 49´19″
C = 25° 10´41″
Aquí te dejamos el video explicativo del tema con ejercicios resueltos.



muyyy buenoo
Muchas gracias por la información tan clara, era lo que estaba buscando.
Nos alegramos Francisco, esa es la idea.
Está buena la página pero no entiendo mucho
daniela muy bonito esta espicable facil de entender
Gracias Daniela.
Creo Que Hay Un Error Al Sumar 2449225+490000 El Resultado Que Pusiste Es=1499225 Y Me Canso De Hacerlo Sumando Y Restando Pero No Me dio Lo Mismo Sumandolo Me Dio =2.939.225 Y Restando Me Dio =1.959.225 ¿Cual El Problema?
En que ejercicio Cesar?
En El Ejercicio #2 Que Hiciste Co Teorema Del Coseno
Solo aplique la formula Cesar. Que parte no entendes?. Fijate bien y revisalo con una calculadora.
Cuando Vas A Sacar El Angulo A
En Un Comentario Arriba Te Puso La Suma Que No Me Da Igual
Que raro yo lo revise.
A mi me dio 1499225 sumando 2449225 + 490000 y restandole 1440000
No se si sea así
Pero así si da
se suma 2.449.225 + 490.000 y luego se le resta a 1.440.000
normalmente el ejercicio se hace mas pequeño y no tanto procedimiento ya que estas haciendo con una calculadora y lo puedes hacer directo el procedimiento sin necesidad de restar numeros demasiado largo como el lo hace
Algunos requieren todos los detalles.
Nunca dejo comentarios, pero estoy tan agradecida, me ayudó bastante y es muy entendible.
Me halaga muchísimo más entonces Andrea
Gracias a ti amigo por fin aprendí el teo. del seno y coseno, es mejor internet que la universidad, saludos
Hola que Dios te bendiga, éxitos.
genial! tenia que repasar para un parcial porque no me acordaba de nada….millloneeeessssss de gracias
Me alegro muchísimo.
QUE BIEN ….. TE NIA QUE PRACTICAR MAS
Si en el ejercicio 2 despues de aplicar coseno q sacas el resultado del lado b aplica el teorema de seno para sacar el angulo A
muchas gracias, m sirvió muchísim, con esto apruebo matemática
Me alegro Benjamín.
En el segundo ejercicio, si saco c con la teoría del seno, ¿esta bien si me da otro resultado? Porque me da 24,83
Ahí puse que no se puede aplicar el teorema del seno de entrada.
En la ley de coseno puedo poner un ángulo de 90 grados
Si hay un angulo de 90° usa pitágoras o las funciones comunes de seno y coseno no los teoremas de seno y coseno porque se trata de un triángulo rectángulo no oblicuángulo
devido a que estos son ejercicios de analisis es bueno practicarlos
tiene sentido
en el ejercicio 1 dice la formula que es b= a2+c2-2ac*cosB en la parte de la resta usted lo puso como suma ¿porque?
Eso depende de los valores del coseno a veces da negativo a veces da positivo
Necesito ayuda tengo un ejercicio k dice
Reducir: sen($+60′)-cos($+30′)
No entiendo por qué algunas veces el terminó -2a.b.cos alfa aparece con signo positivo
Eso tiene que ver con el valor del ángulo. El coseno de ciertos ángulos dan positivos o negativos y ahí se define el signo
Gracias, me sirvió mucho de ayuda el teorema del coseno por que yo sólo tarde horas con diferentes fórmulas y ninguno funcionó hasta que busque y encontré la fórmula para resolver el lado C gracias
Buenísimo Andrés abrazo
el ejercicio 2 esta incorrecto les dejo el link de esta pagina donde dice el verdadero resultado
http://www.vadenumeros.es/primero/trigonometria-resolver-triangulos.htm
No esta incorrecto. Hay solo alguna pequeña diferencia en decimales. Si los lectores ven lo hacen de otra manera. En trigonometría la mayoría de las veces existen más de un camino para resolver los problemas.
una pregunta disculpen mi ignorancia hay alguna manera de comprobar la respuesta en el teorema del coseno
Muy buena la pagina pero hay operaciones que no comprendo todavía
quisiera saber en el ejercicio del seno que operación se hace para quede 0.643 y 0.966 y luego 18 te agradecería que me contestaras en este momento es de carácter urgente. Gracias
La calculadora te saca esos valores maryori. El 0,643 te lo saca la calculadora como todos los demás resultados
el segundo busque el lado c con teorema del coseno, el resto también sale con el del seno.
Disculpen, me podrían ayudar dándome un ejemplo de la ley del coseno aplicado a la mecánica, lo que pasa es que no encuentro nada en la web, relacionado con mi tema
muy buena la informacion gracias bbe
muy buena la informacion gracias bbe penesil
lo
muy bueno agradecida con esto le explico a mi hijo, si el internet hubiera existido cuando yo estudie a lo mejor con esto no hubiera tenido tanto problemas con el calculo en la universidad, pero insistí y me gradué.
Asi es Wilma. Yo tampoco tenía esta herramienta y jamás pense que iba a ser protagonista
Muy buena explicación, Excelente profesor!
Gracias Brisney. Un beso cuidate.
el primer ejercicio lo tienes malo…..asi no se opera
decime en que exactamente.
muy bueno….grciaaaass
De nada Andrés.
Explica muy bien, a mi criterio, pues no me enredo. Yo verifico mi conocimiento viendo otros ejemplos en la web. Gracias
Gracias Claudia queridaaa.
Tal vez es un error mio, pero el angulo A me da 71.80. no se de donde sale 1680000.. en el ejercicio 2.
muy buena información. gracias!!
Para comprobar los ejercicios de triángulos podeis usar TrianCal que está en la web Procomun
Hola Jesús. ¿Es un programa?.