La función cuadrática es un tema muy común en matemática. Se la puede expresar en 3 formas distintas.
Forma polinómica: a X2 + b X + C
Forma canónica: a (X – Xv )2 + Yv
Forma factorizada: a (X – X1) . (X – X2)
Vamos a analizar primero la forma polinómica.
Al estudiar las funciones cuadráticas debemos saber cómo graficarlas y como analizarlas.
Para graficarlas solo basta con conocer los llamados puntos característicos. Estos son las raíces que están ubicadas sobre el eje x, la ordenada al origen, donde la función corta al eje Y. Por último el vértice, para el cual deberemos saber sus coordenadas en X y en Y.
Para encontrar las raíces a partir de la forma polinómica debemos aplicar la ecuación de Bascara. Esta tiene la siguiente forma:
Las letras a y b son los números que acompañan a las x cuadrada y x respectivamente, el c es el término independiente ya que representa a un numero solo sin x. Estas letras se llaman coeficientes
Por ejemplo si tenemos la ecuación cuadrática:
Y = X2 – 2X – 3
Los valores de los coeficientes son: a = 1, b= -2 y c = -3
Reemplazando los valores en la ecuación de Baskara tenemos:
De aquí obtenemos dos resultados con cada uno de los signos.
2 + 4 / 2 = 3
2 – 4 / 2 = -1
Estos valores (1 y -3) son las raíces, es decir son los valores donde la función cortara al eje x.
El valor de corte en el eje Y se llama ordenada al origen y por concepto es el valor donde X vale 0. Si reemplazamos por 0 en las X de nuestra ecuación el valor que obtenemos de corte en el eje y es el -3.
Para hallar el vértice tenemos que encontrar sus valores en X y en Y, o sea, las coordenadas de el vértice.
Vx = – b /2 a
Vx = + 2 / 2.1
Vx = +1
Para el vértice en Y solo reemplazamos el valor de Vx y lo incluimos en la ecuación original.
Y = X2 – 2X – 3
En lugar de Y ponemos Vy y en lugar de X ponemos el valor de Vx
Vy = (+1)2 – 2. (+1) -3
Vy = +1 -2 -3
Vy = – 4
Es decir las coordenadas del vértice son V = ( +1; -4 )
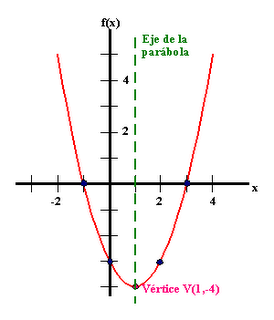
Ahora estamos en condiciones de colocar todos estos datos en una gráfica. La parábola resultante es:
Observamos el eje de simetría que divide a la parábola en dos partes iguales. Este pasa exactamente por el vértice en X. si nos pidieran la ecuación del eje de simetría solo debemos poner:
X = +1
Ya que corta al eje X.
La forma canónica es:
a (X – Xv )2 + Yv
reemplazando las letras que ya las conocemos nos queda:
Y = 1 . (X – 1)2 – 4
Como el 1 no tiene afectación en la función generalmente se los desprecia quedando:
Y = (X – 1)2 – 4
La forma factorizada está formada por el producto:
Y = a (X – X1) . (X – X2)
Y = +1 . (X – 3) . ( X + 1)
Y = (X – 3) . ( X + 1)
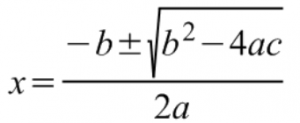
EXCELENTE MATERIAL MUCHAS GRACIAS!!!
Me pareció muy Interesante y que ejemplo tenemos para la Aplicación en la Química.??
Calculo de concentraciones significativas en calculos de pH para electrolitos débiles cuando l concentracion de hidronios u oxhidrilos provenientes del agua no se pueden descartar.
Muy buen material, lo tomo de ejemplo. Gracias!!
Gracias Laura querida.