La Fórmula de Baskara es de enorme utilidad cuando queremos resolver una ecuación de segundo grado.
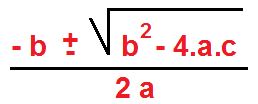
Para entenderla bien y saber que significan esas letras (a,b y c), vamos a ejemplificar con algunos ejercicios.
X² + 4x – 12 = 0
Como observamos, la expresión esta igualada a cero. Esta es una condición que debe cumplirse previamente antes de aplicar la fórmula de Baskara. Las letras antes mencionadas son:
a: Coeficiente principal. Es el número que acompaña al término cuadrático, o sea, a la X². En este caso «1». Cuando hay un número diferente será ese número.
b: Coeficiente lineal. Acompaña al término lineal, en este caso «2».
c: Término independiente. Es el número sin la X. En este caso es «-12».
Una vez identificados procedemos a reemplazarlos en la fórmula de baskara. Nos quedará:

El término b que es 4 queda -4 ya que en la fórmula el b está precedido por el signo menos. Los próximos pasos son resolver el cuadrado y el producto que se encuentran dentro de la raíz y el producto del denominador. Reducida queda así:
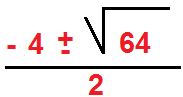
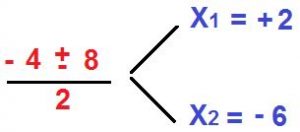
Sabemos que la raíz cuadrada de 64 es 8. Ahora observemos el doble signo +/- que esta delante de la raíz. Eso significa que la solución es doble cuando tenemos una raíz de índice par y radicando positivo como en este caso. En la imagen vemos que las soluciones son: usando el signo positivo: + 2 y con el signo negativo nos da -6.
A continuación te dejo para que practiques lo explicado de la fórmula de Baskara los siguientes ejercicios con su respuesta.
X² – 3x -10 = Rta: X1 = -2 X2 = +5
-X² + 2x + 8 = Rta: X1 = -2 X2 = -4
Profesor: Patricio Arroyo