La estática es la parte de la física que estudia a los cuerpos en equilibrio. Por equilibrio entendemos que la sumatoria de las fuerzas que actúan sobre el es cero. Sin embargo aclaremos que un cuerpo dotado con MRU también sería el caso en donde la la sumatoria de las fuerzas da cero o no actúa ninguna fuerza sobre el mismo.

Aplicando este criterio podremos resolver los problemas en los que se nos presentan para averiguar el valor de una determinada fuerza o la masa de un cuerpo.

Los siguientes ejercicios nos servirán para saber como aplicar lo pasos necesarios para resolver los problemas de estática.

Calcular la fuerza F3 necesaria para mantener el sistema en equilibrio, en donde F1 vale 100 N y F2 vale 40 N.

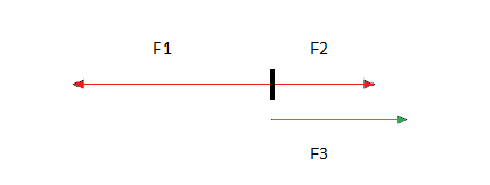
En este caso observamos que la F1 esta hacia la izquierda y las otras dos hacia la derecha. La suma de F2 y F3 deben dar exactamente el valor de la F1 para que el sistema este en equilibrio.

F 2 + F3 = F1

F3 = F1 – F2

F3 = 100 N – 40 N

F3 = 60 N

En el siguiente ejercicio veremos como calcular una de las masas para que el sistema este en equilibrio y la tensión.
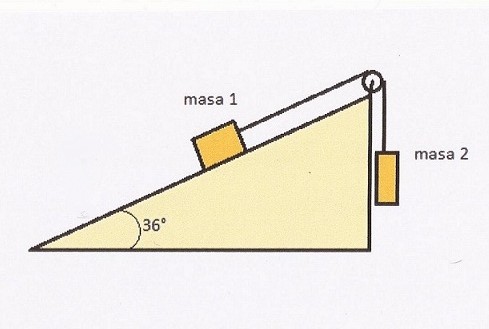Como se observa en la figura, tenemos a dos cuerpos unidos por una cuerda sobre un plano inclinado de un cierto ángulo.

Deberemos hallar el valor de la masa 2 que será necesaria para equilibrar al sistema, así como también el valor de la tensión. Los datos son m1 = 80 kgs y el ángulo de inclinación de 36°.

Es muy importante realizar en estos casos el diagrama de cuerpo libre. Es una gráfica sobre un sistema de ejes ortogonales (x e y), en la que se dibujan todas las fuerzas que actúan sobre el cuerpo y este es representado por un simple punto.

Diagrama para el cuerpo 1.

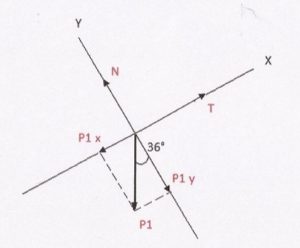
Diagrama para el cuerpo 2.

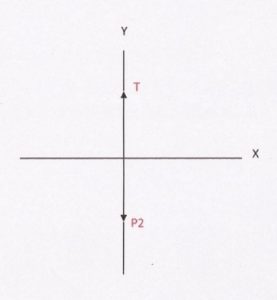
Esto facilita enormemente el cálculo. Aplicaremos la condición de equilibrio desde el principio.

La sumatoria de todas las fuerzas en «x» y en «y» deben dar igual a cero. Después quedaran planteadas las ecuaciones correspondientes en donde despejaremos a las incógnitas.

La fuerzas que actúan sobre el eje x son la tensión y la componente horizontal del peso del cuerpo 1.

Para calcular la componente horizontal del peso aplicamos trigonometría. Es igual al peso por el seno del ángulo.

Fx →    T – P1 . senα = 0

Como el peso es P = m . g

T – m1 . g . senα = 0

Las que actúan en el eje y son el peso del cuerpo 2 y la tensión.

Fy →    T – P2 = 0

T – m2 . g = 0

Quiero aclarar que la tensión es la misma para ambos cuerpos. En otros tipos de problemas de estática, las tensiones son distintas pero no será el caso para estos ejercicios de estática.

Si despejamos a la T de ambas ecuaciones podremos igualarlas y despejar a m2.

De la primera:

T – m1 . g . senα = 0

nos queda:

T = m1 . g . senα

Y de la segunda:

T – m2 . g = 0

nos queda:

T = m2 . g

Por lo tanto si las T son las mismas:

m1 . g . senα = m2 . g

Como las g son las mismas las podemos cancelar y nos queda:

m1 .  senα = m2

m2 = 80 kgs x sen 36°

m2 = 47 kgs

Entonces ahora calculamos a T. Podemos usar la ecuación que querramos.

T = m2 . g

T = 47 kgs . 9,8 m/seg2

T = 460.6 N (Newton)

No te pierdas el siguiente video de Estática para que refuerces loe explicado. Verás el desarrollo de un problema modelo.