Cuando dos rectas transversales son cortadas por dos o más paralelas, se generan entre estas, segmentos proporcionales entre si. Esto es explicado en palabras sencillas el Teorema de Thales.
Sirve para calcular la longitud de dichos segmentos.
Veremos a continuación algunos ejemplos.
1 ) Calcula el valor de los segmentos desconocidos. AB y BC.
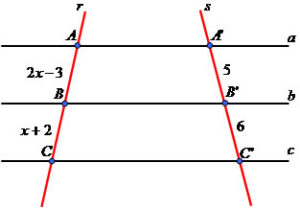
Como se observa, sobre las líneas rojas quedan determinados segmentos. A la izquierda tenemos los segmentos AB y BC y sobre la derecha los segmentos A´B´ y B´C´.
Según Tales se establece la siguiente relación:
AB/BC = A´B´/B´C´
También se puede poner
AB/A´B´ = BC/B´C´
Ahora reemplazamos de la primera relación los valores asignados para despejar x y luego con ese valor de x determinar los valores de los segmentos desconocidos.
2x – 3 / x + 2 = 5 / 6
(2x – 3) . 6 = (x + 2) . 5
Aplicamos propiedad distributiva.
12 x – 18 = 5 x + 10
12 x – 5 x = 10 + 18
7 x = 28
x = 28 / 7
x = 4
Ahora al tener el valor de x solo nos queda reemplazar en las expresiones y calcular el valor de los dos segmentos desconocidos.
AB = 2 x – 3
AB = 2 . 4 – 3
AB = 8 – 3
AB = 5 cm
BC = x + 2
BC = 4 + 2
BC = 6 cm
2 ) Calcula los valores de los segmentos que faltan.
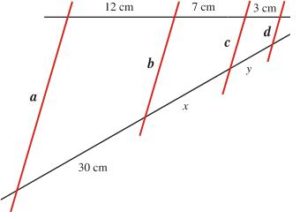
Aquí observamos que faltan el segmento «x» y el segmento «y».
Aplicando la relación de Tales tenemos:
12 cm / 30 cm = 7 cm / x
Despejamos al segmento «x».
x = (7 cm / 12 cm) . 30 cm
x = 17,5 cm
Ahora procedemos a calcular el segmento «y».
12 cm / 30 cm = 3 cm / y
y = (3 cm / 12 cm) . 30 cm
y = 7,5 cm
3 ) Calcular la altura del edificio teniendo en cuenta los otros valores que son, la altura del árbol, la sombra que proyecta este y la distancia entre el edificio y donde termina la sombra del árbol.
El teorema de Thales sirve para resolver este tipo de ejercicios a los que se considera aplicaciones de Tales.
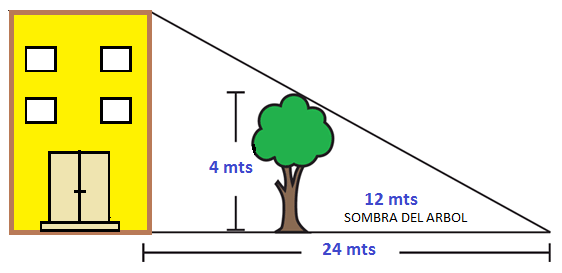
La relación que podemos establecer es la siguiente.
Llamamos x a la altura del edificio. Entonces la altura del edificio es a la altura del árbol como 24 es a 12.
X / 4 mts = 24 mts / 12 mts
X = (24 mts / 12 mts) . 4 mts
X = 8 mts
No te pierdas el siguiente video en donde te explico de nuevo el teorema de tales con más ejercicios para que no te queden más dudas.
41 respuestas a “Teorema de Thales. Problemas resueltos”
Me parecio muy bien sobre estos temas ya que nos ayudan a mejorar nuestra habilidad en las matrmaticas y saludos a Patricio .
Gracias Yenny, sos amorosa.
Hola me auxilias para marcar las rectas transversales y cuales las paralelas en la proporcion de la altura de un edificio y un poste con respecto a la sombra que proyectan.Gracias
Oka pero ¿que datos te dieron?.
me guele a chamullero jsjs
Hueles mal como todo pelotudo
EXCELENTE comentario
Revisa tus errores.
Un Salud
Muchas gracias me sirvió en mi tarea
Me alegroooo.
Hellooo.
En el segundo ejercicio, existe manera de encontrar la longitud de las paralelas a b c d?
Saludos y gracias.
Las paralelas no son parte del problema de tales sino las transversales. Y no, no hay manera.
Gracias La Verdad Que Es Bueno Que La Gente Se Tome Un Tiempo Para Estas Cosas.. Kisses
Me alegro que te sirva. Abrazo.
En el primer ejercicio BC = 6
Gracias César por la corrección, ya lo cambie. Abrazo.
Muchas gracias me pareció súper bien y me ayudó mucho 💙😀
Me alegro Taniii. Besitos.
Gracias, voy para una olimpiada de Matematicas y esto me sirvio.
Excelente Santi.
Muchas gracias patricio eres un grande Patricio y eres muy guapo Patricio, dame tu numero y podemos hacer problemas con muchas x. Muchos besos guapo
Gracias Maria jaja. Para que quieres mi numero?.
hola soy maria pero no se que paso con esto que se borro hasta mi nombre pero te pedia tu numero porque me parecias un profesor muy atractivo y guapo nose si podiamos charlar o no ? quisiera saber .. aparte ..de .. eso…. quisiera saber si me la quieres meter doblada estoy dispuesta alo que sea <3
Sos María y te pones Elverto?.
Aquí ligando bien shido jajajajaja
Muchas gracias, me ayudó mucho, aunque me sigue costando todo esto
No te preocupes Ruth. Estoy a tus ordenes. Doy clases también por si querés saber más.
[…] IMAGEN DEL PRIMER PROBLEMA HASTA: https://quimicayalgomas.com/matematica/teorema-de-tales-problemas-resueltos/ IMAGE DE TRIANGULO RECTANGULO PROBLEMA 2: […]
super bien….DE HECHO YO QUIERO SER QUIMICA <3
Oka. Exitos Yocelin.
Gracias
De nada.
de donde eres broo?
Argentina.
Hola buenas, necesito ayuda 😭
Me dieron lo siguiente:
Aa//Bb//Cc//Dd
El segmento ad=28 cm
Calcular la longitud de los segmentos an, bc, cd
Usando teorema de tales
Era ab
No se entiende, hay que ver el gráfico.
Holi a mi me encantaría aprender más rápido el teorema de thales
Bien gatita
hola necesito ayuda con un problema
María quiere conocer la altura de la torre de la Giralda en Sevilla. Cuando sale a la calle se separa de la base de la torre 8,5 m y observa que para ver el extremo superior necesita un ángulo de elevación respecto a la horizontal de aproximadamente 85°. Si María mide 1,70 m, ¿cuál es la altura aproximada de la Giralda?
Excelente explicación, me ayudó mucho. Gracias.
Gracias Adri.