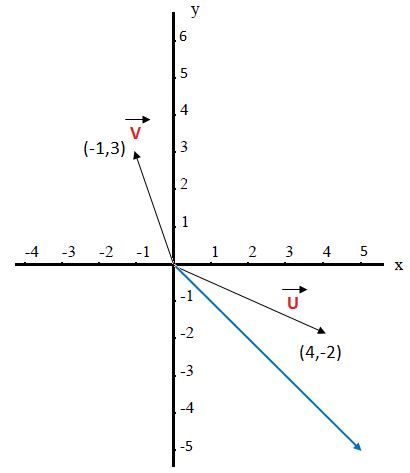
Definición: Un vector es un segmento orientado en el espacio. Se caracteriza por tener:

Un punto de aplicación, en donde nace el vector.
Una dirección, definida por la recta sobre la que se apoya el segmento.
Un sentido, definido por una flecha en el extremo del vector.
Una magnitud o módulo, definido por la longitud del segmento.
Los vectores se suelen representar como flechas de mayor o menor longitud.

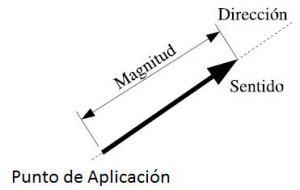
Representación en los ejes coordenados.

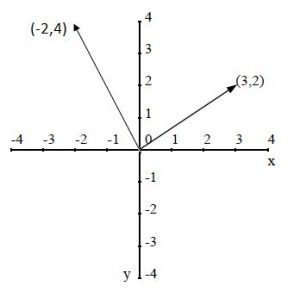
Suma y resta de Vectores:

En el caso de sumar o restar vectores lo podemos hacer gráficamente usando el método del paralelogramo. Por ejemplo si sumamos los vectores del ejemplo anterior obtendremos el vector resultante que se ve de color rojo en el siguiente gráfico. Se lo obtiene trazando paralelas desde las terminaciones de cada vector, líneas paralelas al otro vector hasta que estas se crucen. Así el vector resultante nace desde el orígen y termina en el cruce de las paralelas. La longitud de este vector suma o resultante (en rojo) nos da el valor de la suma de los otros vectores (en negro).

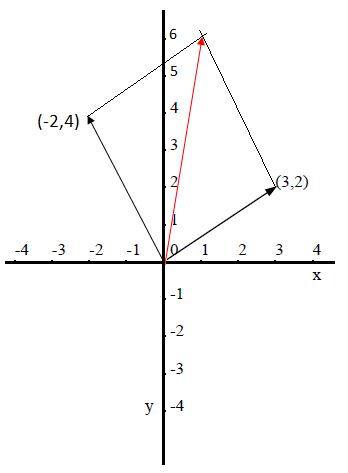
Más sencillo es hacerlo en forma analítica. En estos casos solo sumamos las componentes de cada vector y listo. En este caso observamos en el primer gráfico que las componentes de ambos son:

(3,2) y (-2,4)

Sumamos y nos queda:

3 + (-2) . 3 – 2 = 1. Para la componente X

2 + 4 = 6. Para la componente Y

Vector Resultante: (1 , 6)

Como vemos en el segundo gráfico se nota exactamente que las componentes del vector suma (en rojo) son 1 en x y 6 en y.

En el caso de las restas procedemos de manera similar, solo que en la gráfica no aplicamos el método del paralelogramo salvo que se invierta uno de los vectores (el sustraendo). Por ejemplo si tenemos a los vectores U = (4,-2)  y  V = (-1,3) y nos piden la resta (U – V) en el método analítico procedemos como antes.

U – V = (4,-2) – (-1,3)

U – V = [(4 -) – (-1)] , [(-2)-(3)]

U – V = [4 + 1] – [-2 -3]

U – V = (5 , -5)

El resultado del vector resta es en este caso 5 en X y -5 en Y.