A continuación explicaremos de una manera sencilla el concepto de límite de una función.

El límite de una función en el punto «a» de ¨X¨ es el valor que toma dicha función en el eje «Y» cuando nos acercamos a ese valor en X. Por ejemplo el valor «b».

Es importante aclarar que cuando hablamos de límite, nunca se toma el valor de X en este caso «a». Nos acercamos por derecha y por izquierda pero no se toma el valor. Se observa en la gráfica que cuando nos aproximamos al «a» la función se aproxima al valor «b». Por lo tanto el límite de esta función en el punto «a» es «b».

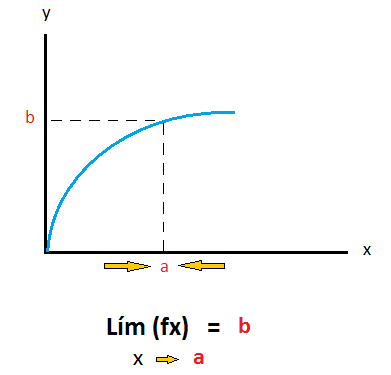
Se lee de la siguiente manera. El límite de la función «f» de x cuando x tiende a «a» es igual a «b».

Hay muchos tipos de límites. Aquí solo veremos algunos ejemplos para que ustedes sepan que hacer cuando se les presenten los diversos ejercicios en donde tengan que calcular el límite de una función.

Les debo aclarar que para calcular límites es de vital importancia conocer algunas herramientas previas matemáticas, sin las cuales es imposible realizar estos cálculos. Por ejemplo, conocer los casos de factoreo. En muchos ejercicios aplicaremos factoreo para poder resolver a los límites.

Ejemplo:

Lo que hacemos es reemplazar a la x por el valor al cual tiende nuestro límite, en este caso 3.

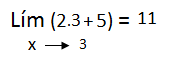
Hacemos el cálculo y encontramos el valor 11. O sea, que el límite cuando esta función tiende a 3 es 11.

El caso que vimos recién es sumamente sencillo ya que lo único que hicimos fue reemplazar el valor de x y listo.

Pero debemos saber que la gran mayoría de los ejercicios de límite no se resuelven tan fácilmente. Veremos que cuando reemplazamos a la x por el valor al cual tienden los límites nos encontraremos con las famosas indeterminaciones. En matemática llamamos indeterminaciones o Límites indeterminados, a aquellas operaciones que no se pueden realizar porque no tienen solución. Hay muchas, pero en este post veremos a dos de las más importantes.  Cero sobre cero, e infinito sobre infinito.

Veremos un ejemplo en donde aplicaremos alguna transformación para cambiar la indeterminación y que sea posible calcular el límite. Cuando cambiamos a dicha indeterminación se le dice «salvar la indeterminación».

En el siguiente ejemplo vemos que al reemplazar la x por el 2 el resultado nos da 0/0.

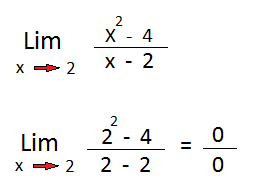
Lo que hay que hacer aquí es factorear a la expresión del numerador. Como vemos se trata de una diferencia de cuadrados. Así que quedara como se muestra a continuación.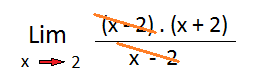

Simplificamos y queda:

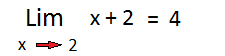
De esta manera hallamos el resultado de un límite que en principio parecía imposible. Como dijimos, es imprescindible que el alumno reconozca y sepa todos los casos de factoreo para encarar a los límites indeterminados.

Ahora veremos un ejemplo de como se resuelve un límite con la indeterminación ∞/∞.

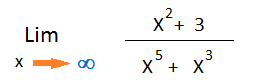
Si reemplazamos a las «X» por el infinito obtendremos la indeterminación mencionada.

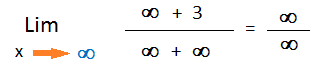
La forma de salvar la indeterminación es dividir a cada término por la X de grado mayor, en este caso la de grado 5.

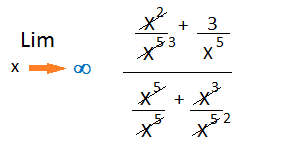
Luego simplificamos ya que tenemos X en los numeradores y denominadores. Quedándonos:

 

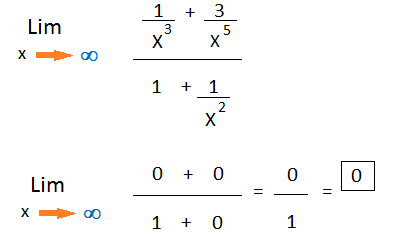
Después nos quedan solo números y finalmente el cero como resultado en nuestro caso.

Quiero aclararles otros casos que se les pueden presentar en estos límites indeterminados.

A veces pueden dar un número sobre infinito. En este caso, el resultado de un número dividido infinito da cero.

Otro caso que se suele observar es un número sobre cero. Si bien sabemos que la división de un número por el cero es indeterminado, es distinto en el caso de los límites. En un límite, un número sobre cero da como resultado infinito. Porque en realidad no estamos dividiendo por cero sino por un valor que se acerca enormemente al cero, lo cual hace que crezca hasta el infinito el resultado.