«Este Artículos fue actualizado el 1 de Agosto de 2025»
El campo numérico está integrado por varias clases de números. A continuación, explicaremos a cada uno de ellos.
Algunos están contenidos a su vez dentro de otro grupo más grande. Los dos grandes grupos de números están formados por los reales y los imaginarios. Ambos forman parte de un campo que abarca a todos llamado números complejos.
Los números reales están formados a su vez por dos clases de números que son los racionales y los irracionales.
Dentro de los racionales tenemos a los enteros y a los fraccionarios o decimales.
Por último, dentro de los enteros, diferenciamos a los enteros negativos y a los enteros positivos, llamados también números naturales.
Para entender mejor la disposición de estos grupos, los resumimos en el siguiente cuadro.
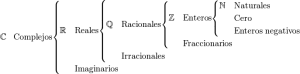
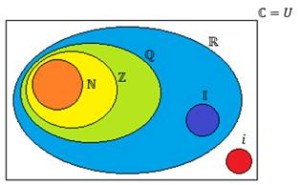
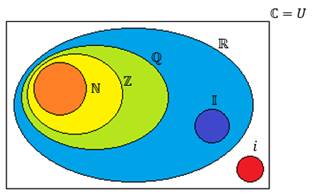
Cada grupo de este Campo numérico esta simbolizado con una letra. Complejos (C), Reales (R), Racionales (Q), Enteros (Z), Fraccionarios (F), Naturales (N), los imaginarios se le asigna la i (minúscula) y a los irracionales la I (mayúscula).
A continuación, daremos algunas características de algunos.
Números Enteros
Cuando hablamos de enteros sabemos perfectamente que son números fáciles de definir porque no admiten decimales después del entero. Por ejemplo, el 2 o el 8 son números enteros. Ahora pueden ser negativos o positivos. Los negativos se ubican a la izquierda del cero y los positivos a la derecha. Por ejemplo:
-4, -3, -2, -1, 0, +1, +2, +3, +4
Los que están a la derecha son mayores que los que se ubican a la izquierda. Por ejemplo -1 es mayor que -3.
Números Fraccionarios
Los fraccionarios son partes (fracciones) de los enteros. Se expresan con dos números separados con una barra. Arriba tenemos al numerador y debajo al denominador. Por ejemplo:
1/2 se lee un medio. Es la mitad del entero. El 1 es el numerador y el 2 el denominador. Otros de ejemplos pueden ser: 1/8 (un octavo), 2/3 (dos tercios), 5/7 (cinco séptimos), etc.
Las fracciones también se pueden expresar como decimales. Por ejemplo 1/2 es lo mismo que 0,5. 2/5 es 0,4 etc.
Tanto los enteros como los fraccionarios o decimales pertenecen al campo de los racionales. Son todos aquellos números que se pueden expresar como razones o fracciones. Los enteros también se pueden expresar como razones. El 2 se expresará como 2/1 o el 5 como 5/1, el 7 como 7/1, etc.
Números Irracionales
Por otra parte, tenemos a los irracionales. Son aquellos que tienen infinitas cifras no periódicas. Como es el caso de la raíz cuadrada de 2 que da 1,4142135…..y siguen infinitamente con variación si tener un patrón de repetición. Así también es el número Pi. π = 3,1515926…
Los Racionales (Q) y los irracionales (I) pertenecen al gran conjunto de los Reales (R).
Números Imaginarios
Por último, para finalizar con el campo numérico, explicaremos de dónde vienen los números imaginarios. Estos surgen por la imposibilidad de calcular las raíces pares de números negativos. Por ejemplo, la raíz cuadrada de 4 es +2 y -2. Pero la raíz cuadrada de -4 no tiene solución en el campo de los reales ya que tanto (+2) y (-2) elevados al cuadrado dan +4. No dan -4 ninguna de las dos opciones. Por lo tanto. en estos casos aparecen los imaginarios. La raíz cuadrada de -4 da como resultado +2 i y -2 i. La unidad imaginaria es la raíz cuadrada de -1 que es 1 i o simplemente i.
Números Complejos (Todo el Campo numérico)
Ahora bien. El campo que abarca absolutamente a todos los números es el Campo de los Complejos. Estos están formados por una componente real y otra imaginaria. Generalmente se los indica con la letra z. Por ejemplo. Z1 = (3 + 4i). Significa que su componente real es el 3 y su componente imaginaria es al 4. En este ejemplo esta como forma binómica. También se puede expresar de otras maneras. Pero el estudio de los complejos merece un post aparte. Solo te lo menciono.
Si te interesó este tema y deseas conocer más información útil, puedes visitar nuestra sección de Temas de Matemática
Cuerpo de números algebraicos – Wikipedia
Hola quisiera saber si saben algo de procesos industriales de reacciones de sustitucion, por favor! Me URGEEEEE :c
Claudia este post es de matemática. Te pido que comentes en los artículos que se relacionen con lo que buscas.
Si que nesesitas
Hola Patricio! Aquí recordando esas clasificaciones en el mundo de los números! Gracias! // Hallo P., sehr gut mit dem Thema: «Zahlen»! Danke sehr!
Gracias querida Dora.
Hola me pueden decir a que campo numerico pertenece estas; y porque
-96.
7sobre/2 .
-24/4.
Raíz de 2
Raíz de -4
Alguien me puede decir a qué campo numérico pertenece el kg y grados celcius y como fundamentada que 50mg es igual a50000ug . Gracias
Kg es unidad de magnitud no un número. Lo mismo celsius
si yo dijo -3.5ºc y 5.800kg dejando de lado la unidad los números en si a que campo pertenecen y por que 50 mg es igual a 50000 ug
3,5 es decimal 5800 es entero. Lee por favor el artículo. 1000 ug es un miligramo por eso son equivalentes.
El conjunto de los números enteros (Negativos y positivos) podría ser un campo numérico? Y si no lo es, dígame por qué. Y muchas gracias por su articulo, es bastante bueno.
Forman parte del campo numérico fijate bien en el artículo que escribí. Gracias.
Ola Queria Saber a Que Campo Numerico pertenece la raiz cuadrada de 2?)
Al mismo campo que todos los otros números. Te referís a que conjunto. Al conjunto de los irracionales. Fijate en la calculadora que te da raíz de 2 y verás cifras no periódicas.