Las ecuaciones con valor absoluto siguen  la misma mecánica que las ecuaciones convencionales, pero con algunas diferencias que explicaremos a continuación.

Antes recordaremos que el valor absoluto de un número tiene en cuenta a los dos signos, el positivo y el negativo. El símbolo del valor absoluto esta representado por las barras verticales que encierran al número o la expresión.

| x | = valor absoluto de x ( – x  y + x )

| 9 | = valor absoluto de 9 ( – 9  y + 9 )

| 6 | = valor absoluto de 6 ( – 6  y + 6 )

Veremos a continuación como encararemos una ecuación en la que obviamente deberemos hallar el valor de la incógnita, que esta encerrada dentro de un valor absoluto.

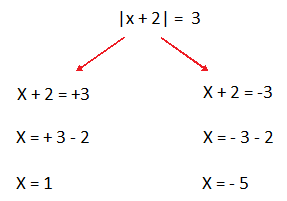
Como se observa, se ponen las dos posibilidades. El valor absoluto contiene a los dos signos. Entonces es mejor colocárselo al número que esta a la  derecha del igual. A la izquierda el +3 y a la derecha el -3. A partir de ahí realizamos los despejes correspondientes. Encontramos los dos valores esperados. A diferencia de las ecuaciones en donde solo encontramos un solo valor.

Ahora veremos el caso de una desigualdad. Es decir, inecuaciones con valor absoluto.

|X + 4| + 1  > 6

Primero nos conviene despejar el valor absoluto.

|X + 4|  > 6 – 1

|X + 4|  > 5

Ahora procedemos como en el caso anterior, con la salvedad de que cuando igualamos al valor negativo invertimos el signo de la desigualdad como se muestra a la derecha. Es decir, a la izquierda vemos que la expresión queda igual pero sin las barras y a la derecha cambiamos el signo del número, en este caso el 5 y el signo de la desigualdad.

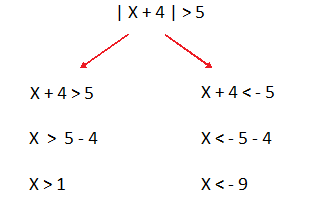
Como vemos, también existen dos resultados con la diferencia de que la solución de una inecuación es un conjunto de valores. Por ejemplo, al decir X > 1 decimos los valores mayores a 1. Pero también tenemos la otra solución que dice X < – 9. Entonces hay que poner la solución general que abarque a todo el rango que cumpla con las dos expresiones.

Finalmente expresamos a la solución como un intervalo.

S = ( -∞ ; 9 ) u ( 1 ; +∞ )