Las Ecuaciones Cuadráticas son aquellas en las que la incógnita es un término cuadrático. Dentro de estas tenemos algunas muy simples y otras algo más complejas para resolver. Veremos a continuación los diferentes casos que se nos pueden presentar a la hora de resolver ecuaciones cuadráticas.
X²- 25 = 0
En este caso simplemente despejamos a la X² moviendo el 25 a la derecha cambiándole su signo.
X² = 25
Después solo nos queda pasar el cuadrado como raíz cuadrada del 25.
X = √25 = +5, -5
Recordemos que la raíz de índice par de un número positivo da como resultado dos valores, el positivo y negativo.
X² + 6x = 0
En este caso tenemos un término cuadrático y otro que tiene una X. En estos casos lo podemos resolver inmediatamente extrayendo a la X como factor común.
X . ( X + 6 ) = 0
Nos queda un producto que da por resultado cero. Cuando un productos da cero, es porque cualquiera de los dos factores da cero. Así que tenemos:
X = 0 y X + 6 = 0
En la segunda expresión (X + 6) despejamos a la X y nos queda:
X = -6
X² + 3X – 10 = 0
Aquí como podes observar, no se puede extraer a la X como factor común. Debemos aplicar algún método para resolver este tipo de ecuaciones. Baskara es el método más común.
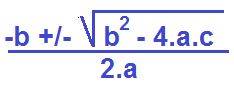
Antes de usar esta fórmula, debemos reconocer los coeficientes a,b y c. Estas letras representan a los números de nuestra ecuación.
a= 1, b= 3, c= -10
Ahora reemplazamos estos valores en la fórmula y la vamos desarrollando.
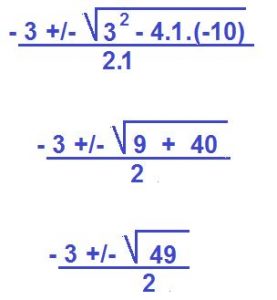
Como observamos, tendremos dos soluciones para esta expresión.
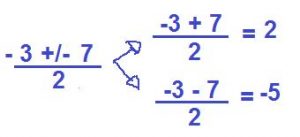
Estas son las dos soluciones. X1 = 2, X2 = -5