La hidrostática estudia las leyes que gobiernan sobre los líquidos estacionados. Por ejemplo, cuando calculamos el empuje recibido sobre un cuerpo que está sumergido o parcialmente sumergido en un líquido o la presión hidrostática que soporta un buzo que descendió cierta cantidad de metros. Las leyes que gobiernan a los líquidos en movimiento están dentro de la hidrodinámica.
Dentro de la hidrostática tenemos al teorema general de la hidrostática.
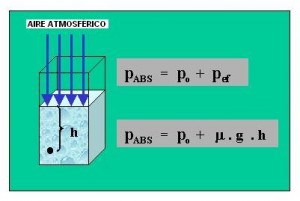
Define la diferencia de presión que existe entre dos puntos s distintas alturas dentro de un líquido. Nos sirve para calcular por ejemplo la presión que soporta un cuerpo dentro del seno de un líquido. La diferencia de presión es igual al producto entre el peso específico del líquido y la altura que hay entre dos puntos distintos.
ΔP = PeL . Δh
Pb – Pa = PeL . ( hb – ha)
A veces la diferencia se establece entre un punto a cierta profundidad y otro situado justo a nivel del líquido en contacto ya con la atmósfera. En este caso como la presión atmosférica es muy pequeña se la puede despreciar. De esta manera se calcula directamente la presión interna del líquido en el punto más profundo.
Pb = PeL . ( hb – ha)
También teniendo en cuenta que el peso específico es igual a la densidad por la gravedad. La formula la podemos ver como:
Ph = D . g . h
Otro punto importante a la hora de evaluar la presión es la unidad en la que la medimos. Hay muchas unidades de presión. Por ejemplo, Pascales (Pa), atmósferas (atm), milímetros de mercurio (mmHg), etc.
Es importante a la hora de resolver problemas que sepamos pasar de una a otra. A continuación citaremos algunas de las más importantes y usadas.
1 atm = 10130 Pa = 101,3 HPa
1 atm = 760 mm Hg
Problemas de Hidrostática:
¿Qué presión soportara un cuerpo sumergido a 2 metros debajo del agua?. D agua = 1 Kg/dm3
P = 1 Kg/dm3 . 9,8 m/seg2 . 2 mts
Debemos transformar la unidad del peso específico del agua a Kg/m3. De esta manera podemos simplificar el metro que acompaña al 2 con un metro de m3 para que quede Kg . m / m2. seg2 donde Kg . m / seg2 es newton (N) una unidad de fuerza. Ésta dividida por m2 da como resultado final al Pascal. Pa = N/m2. 1 Kg/dm3 equivale a 1000 Kg/m3. La presión que resulta es igual a:
P = 19600 Pa
Calcula a qué distancia estará sumergido un cuerpo que recibirá una presión de 2 atm en un líquido de densidad 1.8 kg/dm3. Deberemos convertir las atmósferas a otra unidad de presión.
1 atm = 10130 Pa
3 atm = 30390 Pa = 30390 N/m2
P = D x g x h
h = P / D x g
h = 30390 N/m2 / (1.6 Kg/dm3 x 9.8 m/seg2)
h = 30390 N/m2 / (1600 Kg/m3 x 9.8 m/seg2)
El N es igual a Kg / m.seg2. Simplificando las unidades el resultado queda en metros. El m2 se elimina con dos unidades del m3 quedando un metro libre.
h = 1.93 metros
Principio de Arquímedes
Este principio habla de la fuerza que recibe un cuerpo al ser sumergido en el seno de un líquido. Esta fuerza se llama empuje. La relación fue establecida por el físico griego Arquímedes en el siglo 3 antes de Cristo. Según Arquímedes, el empuje que recibe un cuerpo es igual al peso específico del líquido en el que esta por el volumen sumergido del cuerpo. A veces es el volumen total si este está todo sumergido.
E = Pe x Vsc
Calcula el empuje que recibe un cubo de aluminio de 10 cm de lado si está sumergido totalmente en el agua. (Peso específico Al = 2,7 Kg/dm3).
En primer lugar debemos establecer el volumen del cuerpo. Se trata de un cubo de 10 cm de lado:
El volumen de un cubo es V = l3.
V = (12 cm)3 = 1728 cm3.
El empuje será:
E = Pe x Vsc
E = 1 kg/dm3. 1,728 dm3
E = 1,728 Kg f (kilogramos fuerza)
Si queremos pasarlo a Newton hacemos la conversión:
1,728 Kgf . (9,8 N / 1 Kgf)
16.93 N
Ahora plantearemos el mismo problema pero sin sumergirlo, es decir, arrojamos dicho cuerpo al agua y veremos que ocurre. Se puede hundir o puede flotar. Para esto deberemos calcular el empuje que recibirá y compararlo con su peso que no conocemos. Si el peso es mayor que el empuje se hundirá, si el empuje es mayor o igual al peso este flotara.
El peso específico de un cuerpo es igual a peso dividido por su volumen. Calculemos el peso.
Pe = Peso x V
Peso = Pe/V
Peso = 2,7 Kg/dm3/1,728 dm3
Peso = 1,56 Kgs.
Recordemos que el empuje calculado era de 1,728 Kgf por lo tanto al ser mayor que el peso este flotara.
Otra variante que nos pueden preguntar es que parte del volumen emerge o queda sumergido. Para esto debemos igualar el peso del cuerpo (Pc) y el empuje (E). Teniendo en cuenta que el cuerpo está en equilibrio, es decir la suma de las fuerzas que actúan sobre él es cero.
E – Pc = 0
E = Pc
Según Arquímedes:
E = Pe x Vsc
Pc = Pe x Vsc
1,56 Kgf = 1kg / dm3 x Vsc
1,56 Kgf / 1 Kg / dm3 = 1,56 dm3 o 1560 cm3
Por lo tanto el resto será el volumen emergido.
Ve = Vt – Vs
Ve = 1728 cm3 – 1560 cm3
Ve = 168 cm3
Calcula cuantas personas de un peso promedio de 70 Kgf podrían subir a una balsa de madera cuyas dimensiones son de 4 mts de largo, 2 mts de ancho y 15 cm de alto. Pe madera = 0,75
La condición para que la balsa no se hunda en el agua será de que el empuje que reciba sea igual al peso de esta y de las personas que suban.
Primero calculamos al volumen de la balsa llevando previamente las unidades de longitud a metros para ser homogéneo al cálculo.
V = 4 mts x 2 mts x 0,15 mts
V = 1,2 M3 = 1200 dm3
El empuje que recibe la balsa es de
E = 1 kg/dm3 . 1200 dm3
E = 1200 kgf
El peso del cuerpo será de:
P = Pe x V
P = 0,75 kg/dm3 . 1200 dm3
P = 900 kgf
Vemos que hay una diferencia entre el E y el Pc de:
E – P = 1200 Kgf – 900 kgf
E – P = 300 kgf
Esta diferencia es aprovechada para que suban las personas. Cada persona es de 70 kgf de peso. Por lo tanto se podrán subir unas:
300/70 = 4,29 que redondeando a 4 equivale a 4 personas ya que con 5 personas se sobrepasará el límite.
Artículo: Hidrostática
Muy bueno me ayudó bastante Patricio gracias abrazo!!!
Augusto querido cuidate y éxitos
hola, me puedes ayudar con conceptos de teorema general de la hidrostática y del principio de arquimides
hola. me puedes ayudar . tengo que expresar y esquematizar el teorema general de la hidrostática y del principio de arquimides.
Hola Ruben. De este video puedes sacar la info.