En el artículo de energía cinética explicábamos que la energía mecánica de un sistema, que está compuesta de la potencial y de la cinética tenía una cantidad constante. Dicho de otra manera, la variación de la energía mecánica de un sistema es cero ya que la energía mecánica inicial era igual a la final. Las fuerzas que están presentes en estos sistemas y que no afectan para nada a la variación de energía mecánica se denominan fuerzas conservativas. Su nombre lo indica, conservan y no consumen energía. Si bien producen trabajo físico.
Esto no siempre es así. Hay fuerzas que son diferentes, es decir, consumen energía mecánica al realizar trabajo. Se llaman fuerzas no conservativas. Entre las más conocidas se hallan las fuerzas de rozamiento. A lo largo de una trayectoria, la energía mecánica del sistema se irá consumiendo y la final será menor a la inicial, o sea, su variación ya no será cero.
El valor de la fuerza de rozamiento en física es igual al producto del coeficiente de roce por la fuerza normal.
Fr = µ x N
Hay dos tipos de coeficiente de rozamiento, el cinético o dinámico y elestático. El segundo es mayor en valor. Los valores no tienen unidad y oscilan entre el cero y el uno, mucho más cerca del cero. El µ estático actúa al principio, antes del movimiento y el dinámico actúa durante el movimiento, cuando la inercia se ha vencido. Por esta razón el coeficiente dinámico es de menor valor que el estático.
Otra característica de las fuerzas de rozamiento es que su sentido es contrario al del movimiento del cuerpo. A continuación veremos un ejemplo:
Un cuerpo de 28 Kgs de masa se desliza por un plano inclinado de 35 grados de inclinación que tiene como dimensiones 2 metros de alto. Existe en la superficie un coeficiente de roce de 0.2. Calcular la velocidad con la que llega al suelo.
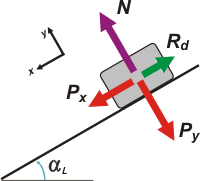
Lo que debemos hacer antes de este cálculo es realizar un diagrama de cuerpo libre. O sea, colocar todas las fuerzas que actúan sobre dicho cuerpo.
Estas son las tres fuerzas que actúan. El peso del cuerpo (P), que como vemos, esta inclinada los 35° del plano inclinado ya que el eje x vendría a representar el lado del plano por donde corre el cuerpo. La normal (N), que es la fuerza perpendicular a la superficie de apoyo que siempre está en todo cuerpo apoyado y la fuerza de roce (Fr) que se opone al movimiento del cuerpo.
La variación de la energía mecánica es igual al trabajo de la fuerza de roce. Por lo tanto primero debemos calcular dicho trabajo.
Wfr = Fr x d
La d es la distancia del plano inclinado. No la tenemos, pero por trigonometría la calculamos. El seno del ángulo es igual a la altura dividido por la d del plano que vendría a ser la hipotenusa de un triángulo rectángulo.
Sen 35° = altura/distancia
D = altura/sen35°
D = 3.49 metros
Ahora sacamos el valor de la F de roce:
Fr = µ x N
El µ lo tenemos pero la N debemos calcularla. En los casos de planos inclinados la N es igual al peso por el coseno del ángulo. Tambien tendremos en cuenta que Peso = masa x g
N = 28 kgs x 9,8 m/seg2 x Cos 35
N = 224.73 Newton (N)
Fr = 0,20 x 224,73 N
Fr = 44,9 N
El trabajo de esta fuerza será:
W Fr = 44.9 N x 3.49 mts
W Fr = 156.7 Joules (J)
La unidad de trabajo y de energía es el J. Ahora si podemos calcular la energía mecánica final restándole a la energía mecánica inicial el valor del trabajo de la F de roce.
Como vemos en el diagrama del plano inclinado, la energía mecánica inicial tiene el valor de la energía potencial ya que no hay energía cinética por no haber movimiento al principio.
EM i = masa x g x h
EMi = 28 kgs x 9,8 m/seg2 x 2 mts
EMi = 548.8 J
La energía mecánica final será:
EMf = 548.8 J – 156.7 J
EMf = 392.1 J
Con esta energía llega el cuerpo al final del plano, es decir, al suelo. Ene ste punto ya no hay altura por lo tanto la energía que queda es solamente cinética:
Ec = ½ masa x V 2
Despejamos la velocidad:
V2 = 2 xEc /masa
Sacamos la raíz cuadrada de esta expresión y nos queda el valor de:
V = 5.3 mts/seg