La Dinámica es la parte de la física en la que se estudian a los cuerpos en movimiento. A diferencia de la cinemática en la que también se estudian a los cuerpos en movimiento, en dinámica si importan las causas de estos movimientos.

Vamos a explicar algunos ejercicios clásicos para que puedan interpretar y saber como resolver los problemas de dinámica.

Las leyes de Newton son las que explican perfectamente a estos problemas. Especialmente la segunda ley de Newton. Esta explica que si una fuerza actúa sobre un cuerpo, este adquirirá movimiento acelerado si esta en reposo, o podrá disminuir su velocidad si esta en movimiento. Es decir que la masa, la fuerza y la aceleración están estrechamente vinculadas.

F = m x a

m = F/a

a = F/m

Son tres expresiones que explican lo mismo. De la primera podemos obtener las otras dos despejando las variables que necesitemos.

1) Calcula la aceleración que tendrá un cuerpo de 8 kgs de masa si se le aplico una F de 120 N (Newton).

Como a = F/m

a = 120 N / 8 kgs

a = 15 m/seg2

Recordemos que la unidad de aceleración es longitud sobre tiempo al cuadrado. Como N (Newton) es Kg x m/seg2 los kgs se cancelan y queda m/seg2.

2) Calcula la fuerza que se le aplico a un cuerpo de 60 kgs de masa si obtuvo una a de 5 m/seg2

F = 60 kgs x 5 m/seg2

F = 300 N.

Otra variable que suele presentarse en estos problemas es la existencia de las fuerzas de rozamiento. Estas se oponen al movimiento como hemos explicado en otro artículo. Veremos ahora como se trabaja en ejercicios en los que se nos presenta este tipo de fuerzas.

3) A un bloque de 28 kgs de masa en reposo se le aplica una F de 200 N y logra ser desplazado sobre una superficie de μ (coeficiente de rozamiento) de 0,2. Calcula su aceleración.

Primero construimos como se ve en la imagen el diagrama de cuerpo libre, para ver bien todas las fuerzas que actúan sobre el cuerpo. Como se ve actúan 4. La normal (N), el peso (P), la F aplicada y la fuerza de rozamiento (Fr).

Como observamos, la F que mueve al cuerpo va hacia la derecha y la fuerza re rozamiento (Fr) va en sentido contrario ya que se opone al movimiento. En este caso la fuerza neta, es la diferencia entre ambas, y es la responsable del movimiento. Ya que si serían iguales la diferencia sería nula y el cuerpo no se movería. Sería un caso de estática y no de dinámica.

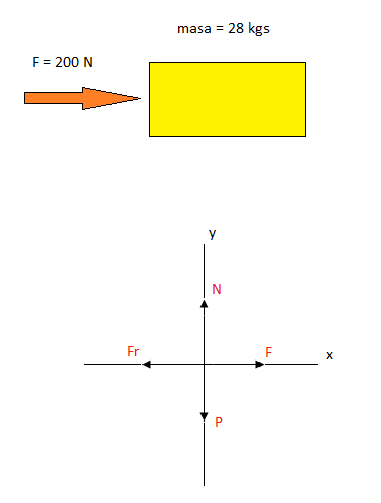
Aplicamos la segunda ley de Newton

F = m x a

Donde F será esta vez la fuerza neta, que es la diferencia entre ambas. Pero antes debemos calcular el valor de la Fr.

Fr = μ x N

La N es igual al peso en este caso, al no ser un plano inclinado.

P = m x g

P = 28 kgs x 9,8 m/seg2

P = 274.4 M

N = 274.4 N

Fr = 0,2 x 274.4

Fr = 54.88 N

F neta = 200 N – 54.88 N

F neta = 145.12 N

La aceleración será:

a = F/m

a = 145.12 N / 28 kgs

a = 5.18 m/seg2

4) Calcula la aceleración del sistema que se indica en la figura.

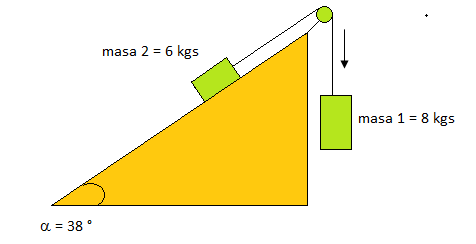
Hacemos el diagrama de cuerpo libre para las dos figuras:

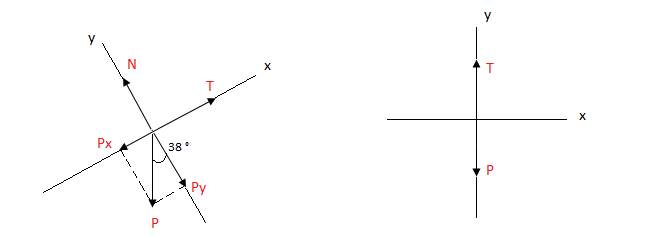
Observamos que el angulo de inclinación que presenta el plano inclinado también se transporta al eje y. La fuerza que hace mover al cuerpo 2 es la tensión a través de la cuerda. Es la misma tensión que se presenta en el diagrama del cuerpo 1 por ser la misma cuerda. Esto será una clave en la resolución del ejercicio.

Ahora plantearemos las ecuaciones de movimiento para cada cuerpo. La segunda ley de newton de nuevo se aplicara.

Cuerpo 1:

Solo se presentan dos fuerzas. La T y el peso de este cuerpo (P1).

P1 – T = m1 . a

m1 . g – T = m1 . a

Cuerpo 2:

Aquí la diferencia entre la T y la Px (componente horizontal del peso), hará que el cuerpo se mueva.

T – P2 x = m2 . a

T – m2 . g . sen α = m2 . a

Ahora sabiendo que la T es la misma para ambos cuerpos, despejaremos a la T.

Cuerpo 1:

T = m1 . g – m1 . a

Cuerpo 2:

T = m2 . a + m2 . g . senα

Igualamos las ecuaciones:

m1 . g – m1 . a = m2 . a + m2 . g . senα

Acomodamos los términos que incluyan a la aceleración del mismo lado:

m1 . g – m2 . g . senα = m2 . a + m1 . a

La a es factor común:

a . ( m1 + m2 ) = m1 . g – m2 . g . senα

a = ( m1 . g – m2 . g . senα )  /  ( m1 + m2 )

a= ( 8 kgs . 9,8 m/seg2 – 6 kgs . 9,8 m/seg2 . sen 38° ) / ( 8 kgs + 6 kgs )

a = 78,4 N – 58,8 N . sen 38°  /  14 Kgs

a = 78,4 N – 58,8 . 0,616 / 14

a = 78,4 N – 36,22 / 14

a = 42,18 N / 14

a = 3 m/seg2