La dilatación lineal es un fenómeno que al igual que la dilatación superficial y volumétrica experimentan los cuerpos cuando hay variaciones en la temperatura. En este artículo hablaremos de la dilatación lineal.
Para entender bien este fenómeno es muy importante entender el concepto de coeficiente de dilatación lineal. Es un número que nos indica en que grado se dilata o contrae un material cuando la variación de la temperatura es de un grado centígrado. Es conocido con al símbolo ∝ (alfa). Y su unidad como hemos dicho es 1/°c. Este coeficiente depende del material que sufra el cambio. Por ejemplo, el cobre, hierro, aluminio, vidrio etc tendrán coeficientes de dilatación diferentes. Los pueden observar en tablas de coeficientes de dilatación lineal en las que figuran lso datos para cada material.
La fórmula que nos da la variación de longitud es la siguiente.

Y la que nos arroja el valor de la longitud final en forma directa es:
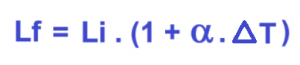
El símbolo ΔT es la variación de la temperatura, es decir, temperatura final menos temperatura inicial). A continuación, veremos algunos ejercicios para entender cómo se aplica esta fórmula.
Calcula la variación de longitud que experimenta una barra de 4 m de cobre si pasa de – 10 °C a 90 °C. El ∝ del cobre es de 1,7×10 a la -5 1/°c. O sea 0,000017 1/°c, como vos prefieras.
Entonces para resolver este ejercicio usaremos la primera formula. Ni siquiera debemos despejar nada porque nos da el resultado en forma directa.
ΔL = 4 m . 1,7.10-5 1/°C . (90°C – (-10°C))
ΔL = 4 m . 1,7.10-5 1/°C . (90°C + 10°C)
ΔL = 4 m . 1,7.10-5 1/°C . (100 °C)
ΔL = 6,8.10-3 m. = 0,68 cm = 6,8 mm.
Esa es la dilatación que experimentará la barra de cobre. Si nos preguntaran la longitud final simplemente le sumamos esta variación a la longitud inicial. Este resultado da 4.0068 m. También podemos aplicar la segunda formula que figura en la segunda imagen. Dará exactamente lo mismo.
Calcula el coeficiente de dilatación lineal del aluminio sabiendo que una barra de 5 m aumenta su longitud a 5.016 m cuando pasa de 6°C a 140°C.
Podemos calcular primero la variación de longitud (ΔL) que es la diferencia entre Lf e Li. 5m – 5,016m = 0,016 m
Ahora despejamos el α de la formula. ΔL = Li . α . ΔT. La variación de T es 140 °C – 6°C = 134 °C.
α = ΔL / (Li . ΔT)
α = 0,016 m /(5 m . 134°C)
α = 2,4 x 10 -5 1/°C
Debes tener en cuenta que a veces el material puede sufrir un acortamiento de longitud. Eso sucede cuando la temperatura disminuye con lo cual tendremos una variación de T negativa. En ese caso hablamos de contracción que sería una dilatación negativa. Pero se aplican exactamente las mismas formulas.
Espero que este post te haya servido. Puedes compartir este material y dejar tus comentarios. Con gusto te contestare. Exitos.
Profesor: Patricio Arroyo.