Las ecuaciones con ángulos tienen como objetivo hallar o determinar los valores de los ángulos que nos piden. Se utilizan generalmente letras griegas igualadas a expresiones que contienen a la letra x. Primero determinamos el valor de esa x. Después una vez obtenido ese valor, lo reemplazamos en las expresiones que nos dieron y encontraremos el valor de los ángulos que nos piden.

Con el siguiente ejemplo verán claramente como se hace. Debemos recordar previamente algunas leyes o relaciones de los ángulos. Por ejemplo la que dice que los ángulos opuestos por el vértice son exactamente iguales. Opuestos por el vértice son aquellos que están formados por las mismas líneas.
Los ángulos suplementarios son aquellos que sumados dan el valor de 180°. Estas dos relaciones son las que imperan en estos tipos de problemas.

Ejemplo:

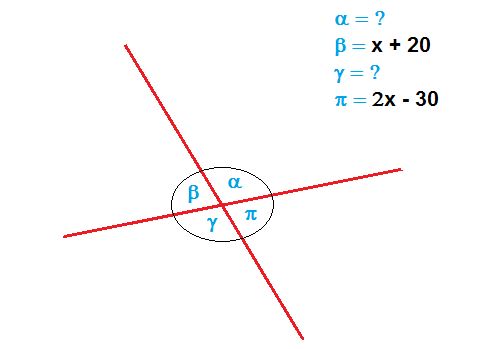
Como observamos, debemos calcular los valores de los 4 ángulos solicitados.
En primer lugar, observamos que tanto β (Beta) como ¶ (Pi) son ángulos opuestos por el vértice y por este motivo medirán lo mismo. No tenemos sus valores pero sus expresiones en función de x. Así que solo nos queda igualarlas:

x + 20 = 2x – 30

Ahora calcularemos el valor de la X con sencillos pasos de despeje.

20 + 30 = 2x – x
50 = x

El valor de x lo reemplazamos en cualquiera de las dos expresiones para obtener el valor de β o de ¶.

β = x + 20
β = 50 + 20
β = 70°

Obviamente Pi vale lo mismo ya que son opuestos por el vértice, lo cual se ve claramente en el dibujo.

Ahora solo nos resta averiguar los valores de α (Alfa) y de γ (Gama).

Ahora podemos observar en el gráfico que alfa y beta son suplementarios ya que es fácil notar que sumados dan 180°. Entonces:

α + β = 180°

α + 70° = 180°

α = 180° – 70°

α = 110°

A su vez hay dos maneras de calcular a gama. Por un lado este ángulo con alfa es opuesto por el vértice, por lo tanto valdrá exactamente lo mismo, 110°. Por otro lado es suplementario de Pi del que sabemos su valor, 70°. Así que si restamos a 180° –  70° nos dará 110°.

De esta manera tenemos ahora todos los valores de los 4 ángulos pedidos.