En este post explicaremos como resolver operaciones con fracciones. Generalmente constituye un tema que da problemas a los alumnos para resolver este tipo de ejercicios.

Las fracciones pertenecen al campo de los números racionales. Estos se suelen expresar de dos maneras, como números decimales o como fracciones. Aquí hablaremos de esta última forma y brindaremos ejemplos concretos de operaciones con fracciones.

Las operaciones básicas son la suma, la resta, la multiplicación y la división.

Suma y Resta de fracciones:

Tenemos dos casos. El más sencillo es cuando los denominadores son iguales. En este caso, la fracción resultante será la misma y el numerador resultante será la suma o resta de los distintos numeradores que aparecen. Por ejemplo, lo podemos verificar en la siguiente suma.

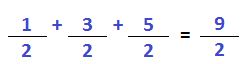
Cuando los denominadores son distintos es más difícil por requerir mayor trabajo, pero no es complicado. Lo que debemos hacer es buscar el famoso común denominador. Es el número que representa a todos los denominadores presentes. Cuando decimos que representa nos referimos a que todos los denominadores deberán estar contenidos en el común denominador que elijamos. Por ejemplo si tenemos al  5  y al 2 el número adecuado es el 10 ya que es múltiplo del 2 y el 5. Si tenemos al 3, al 4 y al 6 el común denominador será el 12. Debemos aclarar que también podría ser el 24 o el 60 pero es mejor elegir al número más pequeño posible. Esto es para facilitar el cálculo posterior.

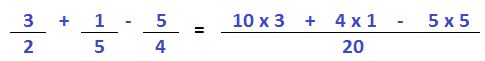
En este caso elegimos al 20 como común denominador. Pero realizamos los siguientes pasos. Dividimos al 20 por el 2, el primer denominador y al resultado este (10) lo multiplicamos por el 3 que es el primer numerador. Luego repetimos estos pasos con los otros numeradores. Obteniendo los productos que se ven en la imagen. Estos productos los resolvemos quedando la operación como se ve a continuación.

El resultado final es 9/20 (nueve veinteavos). Podrán observar que se trato de suma y resta en el mismo ejercicio.

A veces nos encontramos con suma o resta de fracciones con enteros. El procedimiento es el mismo.

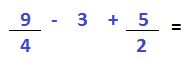
Pero debemos saber o recordar que los enteros tienen como denominador al número 1, por lo tanto lo podemos expresar de la siguiente manera:

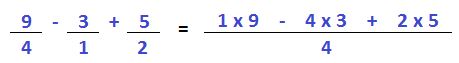
El resto ya lo sabemos. Se elige un común denominador, en este caso al mismo 4, ya que contiene a los tres denominadores.

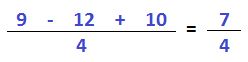
Producto de fracciones: El Producto es sencillo. Se multiplican los numeradores de las fracciones que participan del producto y ese resultado es el numerador de la fracción resultado. Lo mismo se hace con los denominadores.

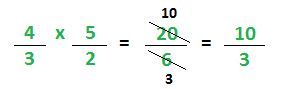
Aquí se observo claramente. 4 x 5 es 20 (numerador) y 3 x 2 es 6 (denominador). Después, si la fracción lo permite se puede simplificar. En este caso al 20 y al 6 lo dividimos por 2 dando 10/3 como resultado final ya que no se puede simplificar más. Recordemos que simplificación es achicar a la fracción dividiendo al numerador y al denominador por el mismo número. Si no encontramos a un divisor común dicha simplificación no se realiza.

Cociente de fracciones:

En el caso del cociente o división de fracciones, la operación es corta. Se realiza el producto cruzado, es decir se multiplica al numerador de una fracción por el denominador de la otra y los dos resultados son el numerador y denominador respectivamente. El numerador del resultado final se obtiene del producto entre el numerador de la primer fracción y el denominador de la segunda. El otro producto cruzado será para el denominador de la fracción resultante. Este orden es importante sino se corre el riesgo de que quede al revés.

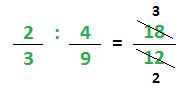
Como se observa, el 18 resulto del producto entre 2 y 9 y el 12 del producto entre 3 y 4. Ese es el orden que hay que respetar y no tendrán ningún problema.

Otra manera de resolver a estas divisiones es simplificar derecho y resolver cruzado, es decir, simplificar numeradores por un lado y denominadores del otro, siempre que se pueda, a veces no se puede. Por último, resolver el producto cruzado como habíamos dicho. El resultado debe ser el mismo de cualquier manera que se haga.

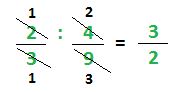
En el producto se puede hacer lo mismo, pero al revés, se simplifica cruzado ( si es posible) y se resuelve derecho.

Estos fueron unos pocos ejemplos pero suficientes para que sepan como proceder en las cuatro operaciones fundamentales con fracciones.