En Trigonometría se habla mucho de las relaciones entre los lados de los triángulos y sus ángulos que estos definen.

A las relaciones entre sus lados, se las llama razones trigonométricas o funciones trigonométricas. En este apartado hablaremos de los triángulos rectángulos ya que en los oblicuángulos las fórmulas son otras y las explicaremos en otro post.

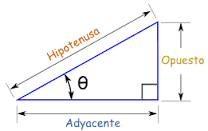
Recordemos como esta formado un triángulo rectángulo. El lado mayor es la hipotenusa, que se encuentra frente al ángulo de 90°. Y los otros dos lados son los catetos.

Explicaremos las tres funciones más importantes por excelencia que nos sirven para resolver los problemas trigonométricos. Estas son el seno, coseno y tangente.

El seno de un ángulo es la relación entre el cateto opuesto a este y la hipotenusa.

El coseno de un ángulo es la relación que hay entre el cateto adyacente de dicho ángulo y la hipotenusa

La tangente de un ángulo es la relación que existe entre el cateto opuesto de ese ángulo y el cateto adyacente a este.

Como vemos es fundamental saber de que ángulo hablamos para definir seno, coseno o tangente. Ya que no es lo mismo la función de un ángulo que la de su ángulo vecino.

 

 

En el gráfico podemos ver y ubicarnos mejor. Por ejemplo para calcular el seno del ángulo θ vemos que será solo dividir el cateto opuesto por el adyacente.

A continuación veremos como hacer algunos ejercicios, tomando como referencia el gráfico anterior para orientarnos bien.

1) Calcular el seno y el coseno del angulo θ del triángulo cuyos datos son:

Cateto adyacente: 6 cm

Cateto opuesto: 4 cm

No tenemos la Hipotenusa. Pero será fácil calcularla a través del teorema de pitágoras ya explicado en un post anterior.

H² = C ady² + C op²

H = √6² + 4² = 7.21 cm

Teniendo la Hipotenusa calculamos el seno y el coseno.

Seno θ = 4 cm / 7.21 cm

Sen θ = 0,555

Cos θ = 6 cm / 7.21 cm

Cos θ = 0.832

Como vimos es sumamente fácil calcular las funciones trigonométricas teniendo los datos adecuados.

Otra cosa que debemos mencionar es que cuando nos piden resolver un triángulo rectángulo lo que nos están pidiendo es calcular todos los lados y todos los ángulos que falten.

2) Calcula el angulo θ, la hipotenusa y el cateto adyacente sabiendo que el otro angulo vale 40°, y el cateto opuesto es de 8 cm.

El angulo θ se calculo teniendo en cuenta una relación muy sencilla que dice que la suma de los tres angulos interiores de todo triángulo (no solo los rectángulos) es de 180°. Como el ángulo recto es de 90°, la suma de los otros dos será también de 90° para completar los 180°. Cuando la suma de dos ángulos es de 90° se dice que son complementarios entre si.

Por lo tanto llamamos β al otro ángulo de 40°.

β + θ = 90°

θ = 90° – β

θ = 90° – 40°

θ = 50°

Ahora calcularemos la hipotenusa y el cateto adyacente.

Para la hipotenusa tenemos dos caminos. Podemos utilizar el seno de θ o  el coseno de β. Ya que en ambos casos tenemos los datos para hacerlo.

Seno θ = cateto opuesto/ hipotenusa

Seno 50° = 8 cm / hipotenusa

Despejamos la hipotenusa, que esta dividiendo. La pasamos multiplicando al miembro izquierdo y queda:

Hipotenusa = 8 cm / seno 50°

Hipotenusa = 8 cm / 0.766

Hipotenusa = 10.44 cm

Veremos ahora como sería si usáramos el coseno de 40°.

Cos 40° = cateto adyacente / Hipotenusa

Hipotenusa = 8 cm / 0.766

Hipotenusa = 10,44 cm

Como vemos da lo mismo ya que el cateto adyacente del ángulo de 40° es el mismo que el cateto opuesto para el ángulo de 50°.

Ahora nos falta calcular el cateto adyacente de θ. La función adecuada para esto es el coseno de θ. O el seno de 40° también funcionará.

Cos 50° = Cateto adyacente/10,44

Cateto adyacente = Cos 50° x 10,44 cm

Cateto adyacente = 6.71 cm

Como vimos en estos dos ejemplos, es fundamental conocer las tres funciones trigonométricas de mayor importancia, seno, coseno y tangente. Son suficientes para resolver a un triángulo rectángulo en su totalidad.

También existen otras tres más, que son las inversas correspondientes a las mencionadas.

Cosecante de un ángulo es la relación entre la hipotenusa y el cateto opuesto de dicho angulo. Es la inversa del seno.

Secante de un ángulo es la relación entre la hipotenusa y el cateto adyacente de ese ángulo. Es la inversa del coseno.

Cotangente de un ángulo es la relación entre el cateto adyacente y el cateto opuesto del ángulo. Es la inversa de la tangente.

Pero repetimos. El seno, coseno y tangente son lejos las más utilizadas para la resolución de los triángulos rectángulos. Aparte son las que figuran en las calculadoras. No así las inversas.

Por último veremos otro ejercicio en donde sabemos el valor de una función pero no su ángulo.

3) Calcula el ángulo θ sabiendo que el cateto opuesto vale 5 cm y la hipotenusa vale 12 cm.

seno θ = 5 cm / 12 cm

seno θ = 0,416666

En estos casos podemos redondear hasta el tercer decimal para no entrar en grandes errores. Nos queda 0,417. Si tomáramos solo dos decimales, nos quedaría 0,41 y ahí si entraríamos en un error considerable. Entonces:

seno θ = 0,412.

El ángulo θ se calcula usando la función inversa llamada arco seno. En las calculadoras se usa el botón schift. El estudiante debe conocer bien su calculadora ya que varían los modelos. Nos quedará:

θ = arco seno de 0,412

θ = 24°19´49″  (24 grados, 19 minutos y 49 segundos)