El campo numérico esta integrado por varias clases de números. A continuación explicaremos a cada uno de ellos.
Algunos están contenidos a su vez dentro de otro grupo más grande. Los dos grandes grupos de números están formados por los Sigue leyendo El Campo Numérico
Operaciones con números complejos
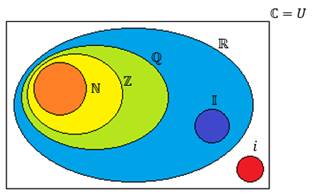
Los números complejos constituyen el campo más grande de los números ya que contienen a todos los reales y a los imaginarios.
Los números imaginarios surgen de la imposibilidad de calcular las raíces pares de los números negativos. Como por ejemplo la raíz cuadrada de -9 no tiene solución ya que ni el +3 al cuadrado ni el -3 al cuadrado daría -9. La unidad imagnaria es «i» y es igual a la raíz cuadrada de -1.
El conjunto de los números complejos se designa generalmente con la letra C. pero en los ejercicios de matemática, a cada uno los vemos simbólicamente con la letra Z. Por ejemplo:
Z1 = 2 + 3i Z2 = -4 + 5i
Vemos que cada uno tiene una parte real y una imaginaria.
Los números complejos están sujetos a las mismas operaciones que practicamos con los números enteros. Suma (adición), Resta (sustracción), Producto (multiplicación) y Cociente (división). A continuación mostraremos ejemplos de Sigue leyendo Números Complejos
