El Cono como todo cuerpo, tiene Superficie y Volumen y debemos saber como se calcula. En el caso de la Superficie podemos observar que la base es circular, por lo tanto responde a la superficie de un círculo cuya fórmula es S = Π.R² ( Pi por radio al cuadrado). Por otra parte tenemos la parte lateral del cono. Esta se calcula con S = Π.R.G (por pi por radio por generatriz). La generatriz (G) es la línea que une el vértice del cono con cualquier punto del perímetro de la base circular.
Por lo tanto el área o superficie total será:
S = Π.R² + Π.R.G
Extrayendo factor común nos queda
S = Π.R.(R + G)

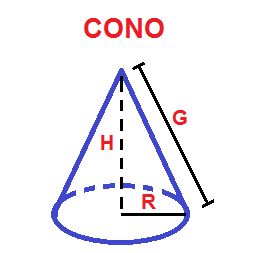
Para el calculo de volumen del cono utilizamos la siguiente formula.

V = (Π.R².H) / 3  (Pi por R al cuadrado por la atura, y todo este producto dividido 3).

Haremos el siguiente ejercicio para aplicar estas formulas y verás que es muy sencillo.

Calcula la superficie y el volumen del cono cuyo R = 20 cm, H = 36 cm.

Para la S necesitamos la generatriz. No la tenemos, pero la podemos calcular teniendo en cuenta que entre el R la H y la G se forma un triángulo rectángulo. Solo debemos aplicar el teorema de Pitágoras. La G es la hipotenusa en estos casos, H y R los catetos. G es la raíz cuadrada de la suma de los cuadrados de R y H. Este cálculo nos da G = 41,18 cm.

S = Π.R.(R + G)

S = 314 . 20 cm . (20 cm + 41,18 cm)

S = 3842 cm²

Para el Volumen.

V = (Π.R².H) / 3

V = 3,14 . (20 cm)² . 36 cm / 3

V = 15072 cm³