El máximo común divisor (MCD) de entre dos o más números es un concepto muy aplicado en matemática. Es el mayor divisor de todos los comunes que tienen. A continuación explicaremos la manera de calcularlo.

Supongamos que tenemos el 18 y el 30, y debemos calcular de los divisores que tengan en común, cual de ellos es el mayor.

18 = 18, 1, 2, 3, 6, 9
30 = 30, 1, 2, 3, 5, 6, 10, 15

Los comunes entre ambos son: 1, 2, 3, y 6. De ellos el mayor es el 6. Por lo tanto el MCD entre 18 y 30 es el 6.

La otra manera bastante frecuente de calcular el MCD es factorizar a ambos números. Esto es, descomponerlos an sus factores primos, o sea, en los números que ya no se puedan dividir más.

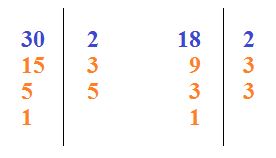
Así nos queda: 30 = 2 x 3 x 5

18 = 2 x 3²

A continuación se tienen en cuenta los factores comunes con el menor exponente y si son más de uno los multiplicamos. Aquí observamos que el 2 y el 3 son los comunes por lo tanto el MCD será:

MCD = 2 x 3 = 6.

Mínimo común múltiplo (MCM).

Es el menor de todos los múltiplos comunes entre dos o varios números.

Usaremos el mismo ejemplo para calcular el MCM (mínimo común múltiplo).

En estos casos se tienen en cuenta los factores comunes y no comunes con el mayor exponente.

30 = 2 x 3 x 5

18 = 2 x 3²

Los comunes en este caso son el 2 y el 3 pero nos quedaremos con el 3² y como no comunes tenemos al 5. Por lo tanto el MCM será:

MCM = 2 x 3² x 5 = 90

De esta misma manera podrán calcular el MCD y el MCM de cualquier grupo de números sin ningún problema.