Las fuerzas paralelas al igual que otras fuerzas, también conforman un sistema de fuerzas llamado Sistema de fuerzas paralelas. Por lo tanto tienen su resultante. Podemos tener fuerzas paralelas de igual sentido o de distinto sentido. A continuación veremos los métodos para determinar las resultantes de los sistemas de fuerzas paralelas.

Sistemas de fuerzas paralelas del mismo sentido: En este caso, la resultante tendrá como modulo o intensidad a la suma de los módulos de las fuerzas paralelas. Se suman por tener el mismo sentido. El punto de aplicación estará más próximo a la fuerza de mayor intensidad y ubicado entre ambas. Para determinar con exactitud este punto, se utilizan dos métodos. El gráfico y el analítico que representa el uso de la relación de Stevin.
Método gráfico:

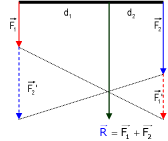
Observamos que donde termina una fuerza colocamos la otra. Es decir, trasladamos la F2 al extremo de F1 y la F1 al extremo de F2.  A continuación unimos los extremos de las mismas fuerzas que se encuntran en frente. O sea, el extremo de F1 con la de F1´y el extremo de F2 con el de F2´.Donde se cruzan los líneas se traza la resultante (R). Y el extremo de la R coincidirá con la suma de ambas fuerzas.

Otra manera de hacer esto sin necesidad de graficar es usando la relación de Stevin. Cuya fórmula es:

F1 / d2  =  F2 / d1  =  R / (d1 + d2)

Si conocemos por ejemplo ambas fuerzas ( F1 y F2), y la distancia total, (d1 + d2) sin conocer d1 y d2. Podemos determinar a estas distancias ya que al igualar  F1 / d2 = R / d, despejaremos d2 sin ningún problema. Sabiendo d2 obviamente sabremos d1 ya que  d1 + d2 = d,  y podemos trazar la R en el lugar adecuado.

Sistemas de fuerzas paralelas de distinto sentido: En estos casos las paralelas son de distinto sentido o sentido contrario. Aquí el módulo de la R será la diferencia entre ambas fuerzas. Por ejemplo si una apunta hacia arriba y vale 80 Kgf y la otra hacia abajo y vae 60 Kgf la R valdrá 20 Kgf. ahora bien, la ubicación de la R no estará entre ambas fuerzas, a diferencia del sistema de furzas paralelas de igual sentido.
A continuación mostraremos el siguiente gráfico:

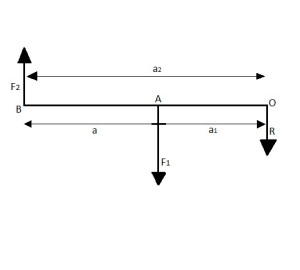Aquí vemos como la R esta a la derecha de F1 que es la mayor de las fuerzas. La a, es la distancia entre las F1 y F2. La a2 es la distancia entre F2 y R y la a1 la distancia entre F1 y R. Esto también se puede determinar por el método de Stevin. El alumno podrá verificar con el siguiente ejercicio la aplicación de la relación de Stevin.

Aplicando al esquema anterior los siguientes valores:

Las fuerzas en Newton. F2 = 40 N,  F1 = 60 N,  a = 40 cm

Calcular las d1 y d2 correspondientes y el módulo de R.

Resultados:

a1 = 80 cm, a2 = 120cm, R = 20 N.

No te pierdas el video siguiente. Clasificación de Sistemas de Fuerzas, ejemplos y ejercicios resueltos.