En física llamamos al movimiento de una partícula o un cuerpo tiro parabólico o tiro oblicuo cuando su trayectoria describe una parábola. Las leyes que describen este movimiento las detallaremos a continuación y como veremos se derivan de las que rigen al tiro vertical y caída libre.

 

Un típico ejemplo de este tipo de trayectorias es el disparo de una bala de cañón. Sabemos que tiene un movimiento ascendente a partir de cierto ángulo y luego desciende simétricamente como ascendió. Las preguntas típicas en los problemas de tiro oblicuo son: ¿Qué distancia horizontal recorrió la bala?. ¿Cuál fue su altura máxima?. ¿Qué tiempo demora en hacer el recorrido horizontal (alcance)?. ¿Qué velocidad lleva luego de 5 segundos de haber sido disparada? Etc.

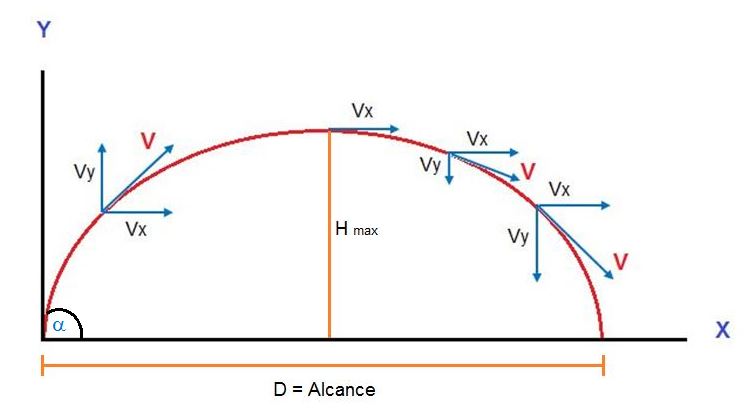
Como observamos en el gráfico la dirección de la velocidad es tangente a la curva en todo punto de la trayectoria. Este vector que representa la dirección de la velocidad se puede descomponer en “x” y en “y”. La velocidad en x (Vx) no cambia su intensidad, es la misma en todo el viaje. La velocidad en y (Vy) es variable ya que sufre el efecto de la gravedad que actúa en vertical, sobre la misma dirección de y.

La Vx es la componente horizontal de V, y por trigonometría sabemos que:

Vx = V . cos a

Vy = V . sena

Sabemos que si la velocidad no varía en un camino se trata de un MRU. La distancia en este tipo de movimiento es d = V . T

Entonces el recorrido lateral de un proyectil de tiro parabólico será:

D = Vx . T

D = V . cosa . T

Para averiguar la altura máxima alcanzada que sabemos es el vértice de la parábola, lo haremos con esta fórmula:

H máx = (Vi . sen a)² /  (2 . g)

Observamos que (Vi . sen ) es la que aparece ya que es Vy la que le dará altura al cuerpo disparado.

Otra fórmula muy importante es la del tiempo. Nos piden tiempo de altura máxima y tiempo de alcance.

El tiempo de altura máxima (T _HM)lo deducimos del tiro vertical. En el tiro vertical el tiempo de altura máxima es cuando la velocidad se hace nula. Entonces si Vf = Vi – g.t queda:

0 = Vi – g.t

Despejando el tiempo queda:

T = Vi / g

La adaptamos al tiro oblicuo haciendo la salvedad que la Vi es la velocidad inicial pero de la componente vertical quedando:

T _HM = Vi . sen a / g

El tiempo de alcance (T_A), o sea, el tiempo que tarda en recorrer la máxima distancia horizontal recorrida, será exactamente el doble que el anterior ya que como podemos ver las parábolas son simétricas. El mismo tiempo que tarda en subir tardara en bajar.

T _A = 2 . (Vi . sen a) / g

Por último, en los problemas de tiro parabolico a veces nos preguntan qué velocidad tiene cierto objeto luego de unos segundos de ser lanzado. En este caso tendremos que determinar si está en la parte ascendente o descendente de la trayectoria. Luego determinar las componentes x e y de las velocidades y por último calcular V que vendría ser la hipotenusa en la relación pitagórica. Como Vx nunca varía podemos usar la misma si se la ha calculado ocn anterioridad. Determinar Vy es más largo. Ya que Vy como dijimos anteriormente va variando con g. para determinar Vy en un cierto tiempo, debemos usar la fórmula Vf = Vi – g.t Particularmente si está en la zona ascendente usamos el signo menos por ir en contra de la dirección de g. Quedara Vy = Vi.sena  – g.t. una vez determinada Vy y Vx calculamos la V total, la que va en la dirección tangente a la trayectoria con la relación de Pitágoras:

V = √ (Vi²  +  Vx²)

Calcula el tiempo total de vuelo y la altura máxima de un cuerpo que fue lanzado con una V de 120 m/seg y con un ángulo de 36° sobre la horizontal.

El tiempo de vuelo total es

T = 2 . Vi . sen a /g

T = 2 . (120 m/seg . sen 36°) / 9.8 m/seg²

T = 14,4 seg

La altura máxima será:

H máx = (Vi . sen a)² /  (2 . g)

H máx = (120 m/seg . sen 36°)² / (2. 9,8m/seg²)

H máx: 26.59 m

Un objeto es lanzado con un ángulo de 42° y una velocidad de 140 m/seg. Determinar el alcance y la velocidad total luego de 2 seg de haber sido lanzado.

El alcance es

D = V . cos a . T

Tenemos la velocidad pero no el tiempo de alcance. Debemos primero determinar dicho tiempo.

T_A = 2 . Vi . sen a /g

T_A = 2 . (140 m/seg . sen 42°) / 9,8 m/seg²

T_A = 19.12 seg

Ahora determinamos el alcance:

A = 140 m/seg . cos 42°. 19.12 seg

A = 1989.25 metros.

Para la velocidad total a los 2 seg como dijimos antes debemos tener los valores de Vx y de Vy justo a los 2 seg. Vx no varía nunca por lo tanto:

Vx = V . cos 42°

Vx = 140 m/seg . cos 42°

Vx = 104 m/seg

Para Vy usaremos la fórmula Vy = Viy – g.t

Velocidad en Y es igual a velocidad inicial en y menos gravedad por tiempo.

Vy = Vi . sena – g.t

Observamos que a los 2 seg el cuerpo esta en etapa ascendente ya que el Ta dio unos 19 segundos por lo tanto el T de altura máxima sería la mitad. Un valor más alto que los 2 segundos que nos piden.

Vy = 140 m/seg . sen 42° – 9.8 m/seg².2 seg

Vy = 93.68 m/seg – 19.6 m/seg

Vy = 74.1 m/seg

Ahora calculamos el valor total de V:

V = √ (104m/seg)² + (74.1 m/seg)²)

V = 36.28 m/seg

No te pierdan el siguiente video de Tiro Oblicuo para que no te queden más dudas.